Определение количества подаваемых вагонов двум клиентам промышленным железнодорожным предприятием, страница 3

Таблица 10.23

	И		К		Л		М
З	∞								68
	0						∞
И			37						0
	∞		0		37
К	0				37				0
	0		∞		0
Л			0				∞		0
	37		0		∞		0
	0		0		0		84		152

Маршрут движения коммивояжера:

S[ИЗ, ЗЖ, ЖЕ, ЕД, ДГ, ГВ, ВА, АБ, БМ, МЛ, ЛК, КИ] = 1102 км

11. Решение задачи этапного распределения ресурсов методом динамического программирования

Исходные данные:

Таблица 11.1

Решение задачи оптимального распределения ресурсов начинаем с последнего 6 этапа, предполагая, что к началу этапа имеются ресурсы К₅, истинная величина которых неизвестна.

при  .

Данная задача представляет собой простейшую задачу линейного программирования, которая решается известными методами. В целевую функцию  входит с коэффициентом 0,64, большим, чем остальные коэффициенты. Следовательно, чтобы максимизировать функцию  необходимо принять: Тогда .

Такое решение означает, что распределяемые ресурсы К₅ следует вложить в станцию 4. Полученное решение является условным, поскольку истинное значение ресурсов К₅ пока неизвестно.

Ресурсы К₅ являются остатком ресурсов в конце четвертого этапа.

Если подставить значения функций остатка из условия задачи, то получим

Найдем значение дохода  через ресурсы 4 этапа К₄, подставив в полученное решение значение К₅.

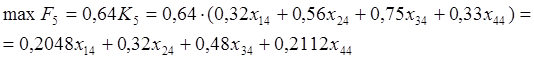
Далее перейдем к максимизации дохода на двух этапах (4 и 5):

при

Подставив значения max F₆и функции дохода из условий задачи, получим:

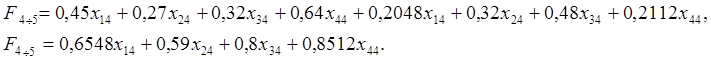
при условиях

В целевую функцию  входит с коэффициентом, большим, чем остальные коэффициенты. Следовательно, будет при т.е. ресурсы К₄ необходимо направить на объект 4. При этом

Выразим ресурсы К₄ через ресурсы третьего этапа. Поскольку ресурсы К₄ являются остатком ресурсов 3 этапа, то:

Запишем полученное на 4 этапе решение:

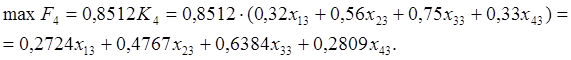
Далее перейдем к максимизации дохода на двух этапах (3 и 4):

При

Подставив значения max F₄ и функции дохода из условий задачи, получим:

при условиях

Коэффициент прив целевой функции больше всех остальных коэффициентов. Следовательно, будет  т.е. ресурсы К₃ необходимо направить на объект 3. При этом 

Выразим ресурсы К₂ через ресурсы 3 этапа. Поскольку ресурсы К₃ являются остатком ресурсов 2 этапа