Т.к. с каждой ячейкой производятся одни и те действия (проверяется, является ли значение ячейки отрицательным и четным числом), то лучше всего оформить работу с ячейками в виде цикла. Т.к. четко известно, сколько ячеек нужно обработать, то используем цикл с конечным числом повторений.
Алгоритм решения:
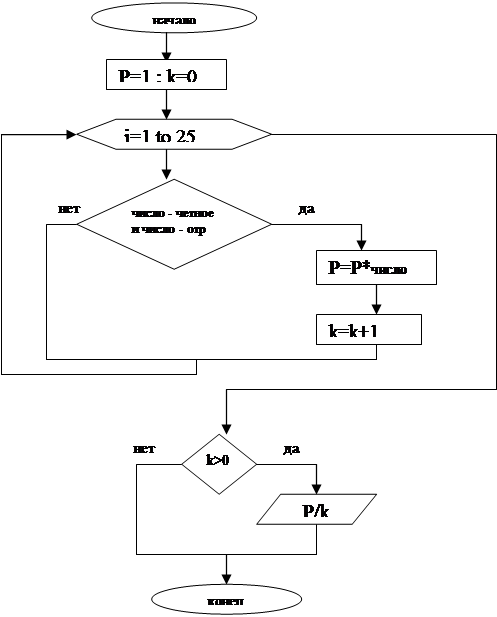
1. Объявим переменные: Р – произведение чисел; k – количество чисел, удовлетворяющих условию, i – номер строки, в которой находится ячейка.
2. Переменной Р присваиваем значение , равное 1, чтобы в цикле можно было наращивать произведение. Переменной k присваиваем 0
3. Проанализируем каждую ячейку в цикле. Значения ячеек, удовлетворяющих условию, добавляем в произведение и подсчитываем.
4. Если имеются числа, удовлетворяющие условию, находим среднее геометрическое.
 |
 Программа:
Программа:
2.3.
 |
Сортировкой чисел назовем процесс перестановок чисел, в результате которого числа будут расположены по возрастанию или убыванию.
На данный момент существует множество разнообразных видов сортировок, в той или иной степени рациональных. Рациональность метода сортировки определяется временем, которое затрачивается на упорядочение чисел.
Все сортировки, известные на данный момент, являются модификацией или комбинацией трех базовых методов сортировок: сортировки обменом (пузырек), сортировки выбором, сортировки вставками.
Рассмотрим два метода сортировок: обменом и выбором.
2.3.1. Сортировка методом обмена (пузырьком)
Задача. Отсортировать 15 случайных чисел, расположенных в столбце А, по возрастанию методом обмена.
Для того чтобы понять, как работает метод пузырька, удобней расположить числа в столбец. Рассматривать числа будем снизу вверх, сравнивая каждую пару чисел. Если ниже расположенное число меньше выше расположенного, меняем их местами. В результате таких сравнений и обменов, за один проход по столбику чисел на самой верхней позиции будет располагаться минимальный элемент (минимальный элемент всплывает вверх).
Чтобы полностью отсортировать числа, в самом худшем случае потребуется 15 проходов по столбику чисел.
Алгоритм решения:
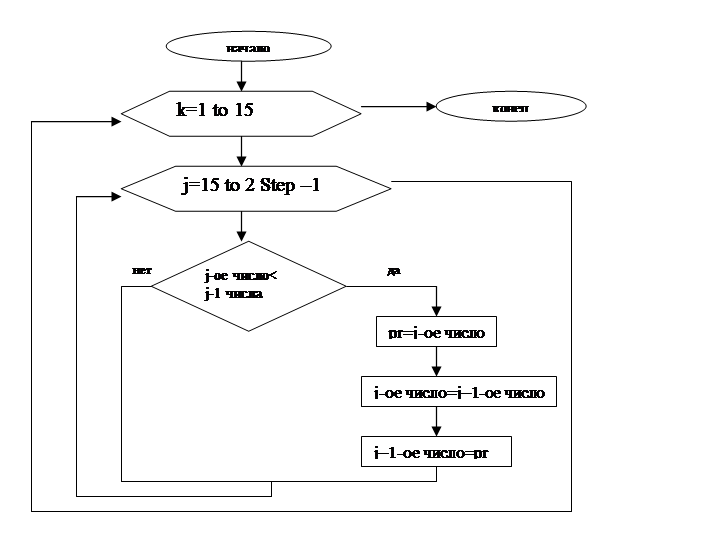
1. Объявим переменные: j – номер числа, с которым будет сравниваться предыдущее число; pr – промежуточная переменная, необходимая для того, чтобы удобней было производить обмен чисел, k – число проходом по столбцу чисел.
2. Организуем два вложенных цикла FOR.
Внутренний цикл будет отвечать за единичный проход по столбцу, при котором будут сравниваться каждые два рядом расположенные числа. Т.к. сравнение ведем снизу вверх, и число сравнивается с предыдущим, то цикл организуем от 15 до 2 с шагом –1.
Внешний цикл будет подсчитывать число проходов по столбику.
Блок-схема:
 |
 |
||
2.3.2. Сортировка методом выбора.
Задача. Отсортировать 15 случайных чисел, расположенных в первой строке, начиная с ячейки А1, по возрастанию методом выбора.
Это самая интуитивно понятная сортировка.
На первом проходе по столбику чисел выбирается минимальный элемент и ставится на первое место.
На втором проходе из оставшихся 14 чисел опять выбирается минимальный элемент и ставится на второе место и т.д., т.е. на каждом проходе из оставшихся неупорядоченных чисел выбирается минимальный элемент и переставляется к началу.
Алгоритм решения:
1. Объявим переменные: min – для хранения минимального на каждом проходе числа; m –номер минимального элемента; j – номер числа, с которым будет сравниваться min; k – счетчик проходов по строке чисел; pr – промежуточная переменная, необходимая для удобства обмена минимального элемента и элемента, стоящего в начале строки.
2. Организуем два цикла FOR: во внутреннем цикле будем находить минимум среди не отсортированных чисел и запоминать индекс минимального элемента (это необходимо сделать, чтобы осуществить обмен). Внешний цикл будет подсчитывать число проходов по строке чисел, и переставлять минимальный элемент в начало строки.
![]()
![]()
![]()
![]()
![]()
|
|
 |
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|

|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.