Анализ переходных процессов. Вариант № 2, страница 2

i₅(0+) = К_I* i₁

i₅(0+) =1/3*7,2 = 2,4

i₅(0+) = i₅(уст) + i₅(св)

2,4 = 4 + i₅(св)

i₅(св) = 2,4-4 = -1,6

Ответ: i₅(t) = 4-1,6*е^-(t/5)

Задача 2.2.

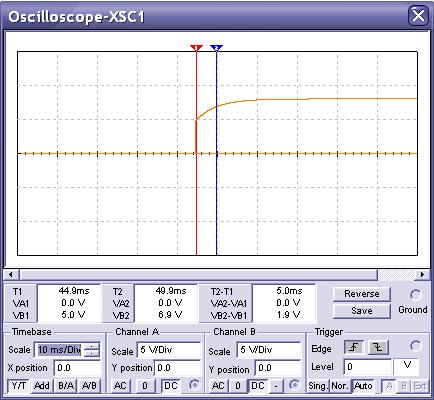
В момент времени t = 0 в цепи замыкается ключ К. Определить независимые начальные условия и найти  u₂(0+), u₂(уст), u₂(св). Построить график u₂(t).

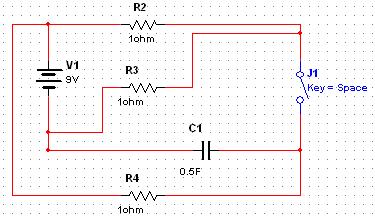
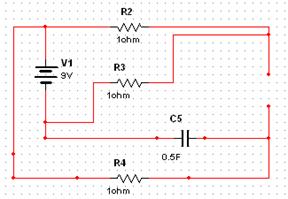
Цепь: 114-ИН; U₁ = 9; 212-R₂; 324-R₃; 413-R₄; 534-C₅ = 0.5; 623-K; замыкается. Найти u₂.

Схема:

Решение.

Будем искатть решение в виде:

u₂(t) = u₂(уст)+ u₂(св)e^pt

1. Определим постоянную времени .

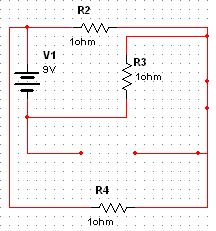
Составим схему замещения для определения R_e относительно точек a и b:

               

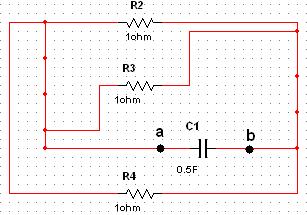
R_e = 1/3.

Из уравнения p = -1/(R_e*C):

p = -3/0.5 = -6

Постоянная времени  = -1/p:

 = 1/6

2. Определим напряжение на конденсаторе до коммутации u_С(0-).

          

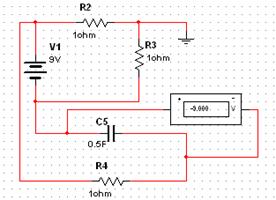
u_С(0-) = -9

3. Определим постоянную составляющую напряжения u₂(уст) в установившемся режиме цепи.

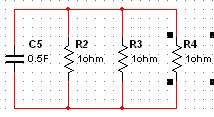
Составим схему замещения:

                 

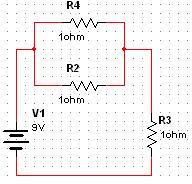
R_e = (R₄ || R₂) + R₃ = 1/2+1 = 1.5

K_U = R₂₄/(R₂₄+R₃) = 0.5/1.5 = 1/3

u₂(уст) = U₁* K_U = 9*1/3 = 3

4. Определим свободную составляющую напряжения u₂(св).

По схеме замещения определим «скачок» напряжения в момент времени t = 0+.

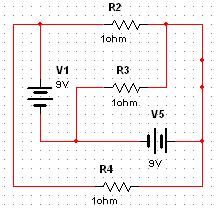         Рассмотрим контур U₁-R₂-U­₅. Очевидно, что потенциалы на зажимах резистора R₂ равны между собой и равны 9. Следовательно, напряжение u₂(0+) = 0.

u₂(0+) = u₂(уст) + u₂(св)

0 = 3+ u₂(св)

u₂(св) = -3

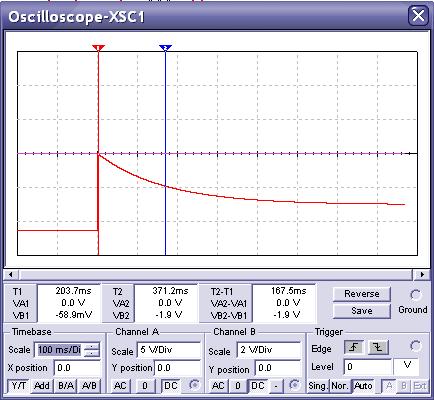
Ответ: u₂(t) = 3 – 3*e^-6t_.