Финансовые функции. Расчет доли платежей кредитов тремя способами

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное учреждение

 высшего профессионального образования        

«Дальневосточный государственный университет путей сообщения»

Лабораторная работа №1

ФИНАНСОВЫЕ ФУНКЦИИ

Выполнила: Мубинова В.А.

311гр

Проверил: Ланец С. А.

Хабаровск 2014

Цель работы: научиться рассчитывать доли платежей кредитов тремя способами.

Ход работы

Способ 1

1. Задаём условие в ячейках

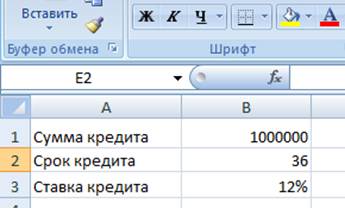
2. Строим таблицу с шапкой в ячейках

3. Расставляем номера месяцев

( от 1 до 36)

4. Первый способ расчета погашения кредита – дифференцированный платеж. Дифференцированный платеж - это платеж с одинаковыми частями погашения основного долга, то есть выплата основного долга не изменяется от месяца к месяцу. 

5. Сумма на начало месяца в первой ячейке – начальная сумма кредита, делаем ее постоянной ссылкой.

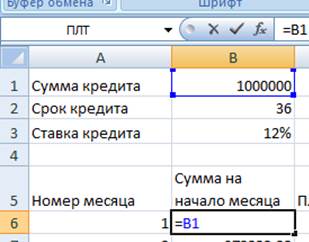
6. «Платежей по %» = «сумма на начало» * «Годовая ставка кредита»/12. При этом «сумма на начало»  делаем переменной ссылкой,  т.к. она будет меняться от месяца к месяцу, а «Годовая ставка кредита» делаем постоянной ссылкой.

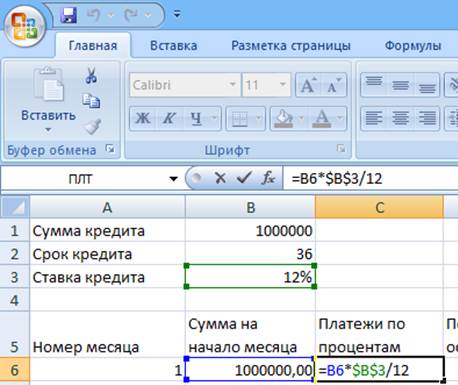
7. Погашения основного долга - не меняется от месяца к месяцу. Поэтому «Погашение основного долга» = «Начальная сумма кредита»/ «срок кредита в месяцах» (делаем их постоянной ссылкой).

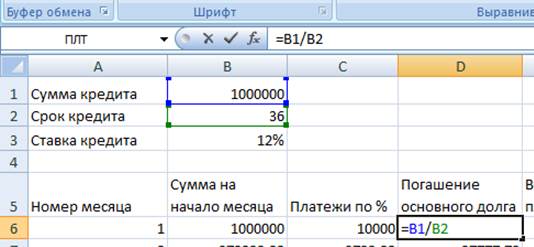
8. «Всего платежей» = «Платежи по %» +  «Погашения основного долга». Делаем их относительными ссылками.

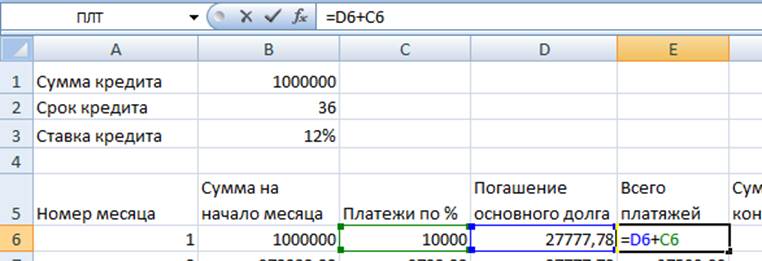
9. «Сумма на конец» =  «Сумма на начало»  - «Погашения основного долга». Делаем их относительными ссылками.

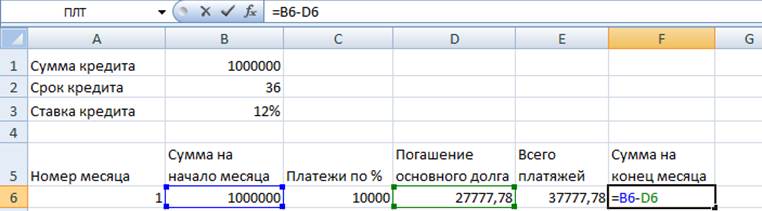
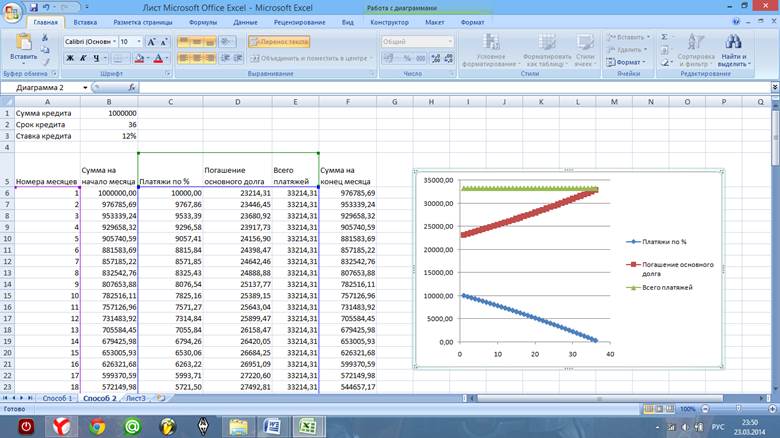
10. Растягиваем всё и полученная таблица и график.

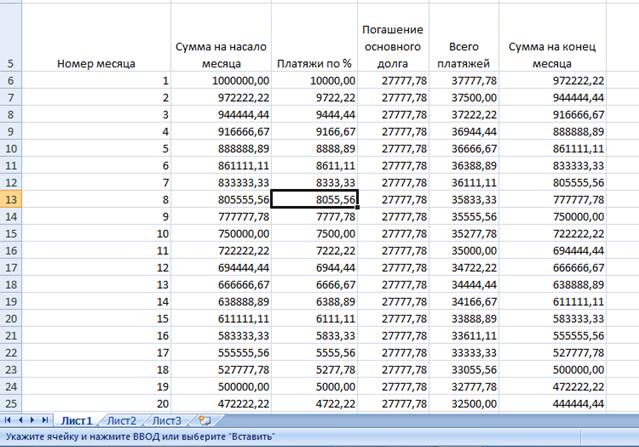
11. Создаём график.

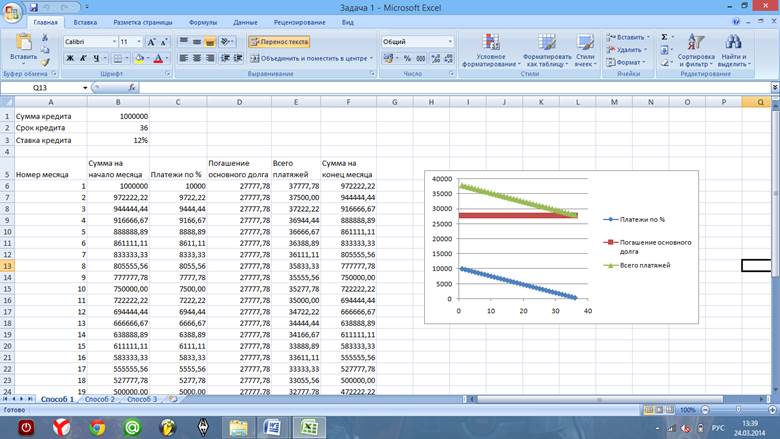
Способ 2

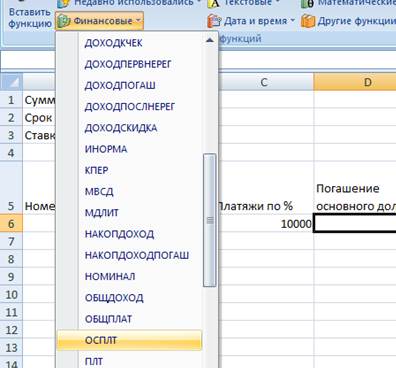
1. Второй способ погашения кредита – аннуитетный, то есть с постоянными суммарными выплатами = % по кредиту  за месяц + погашения основного долга = постоянная величина, и расчёт будет производиться с помощью стандартной финансовой функции ОСПЛТ. Следовательно, копируем таблицу расчета дифференцированного кредита.

ОСПЛТ - возвращает величину выплат на основной капитал для вклада в заданный период.

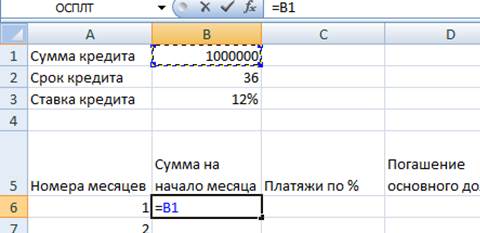
2. Поменяем формулу для расчета основного долга в первом и во втором месяце.

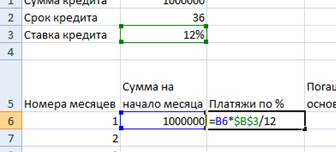
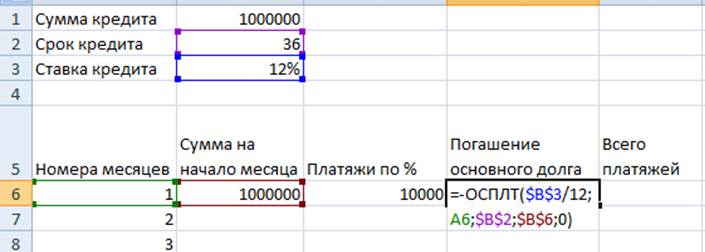
3. «Погашение основного долга» = -ОСПЛТ(«годовая ставка в %»/100/12; «Сумма на начало»; «Срок кредита»; «Начальная сумма кредита»). Причем «Годовая ставка в %», «Срок кредита» и «Начальная сумма кредита» - абсолютные ссылки, а «Срок кредита» - относительная. Погашение основного долга является постоянной величиной.

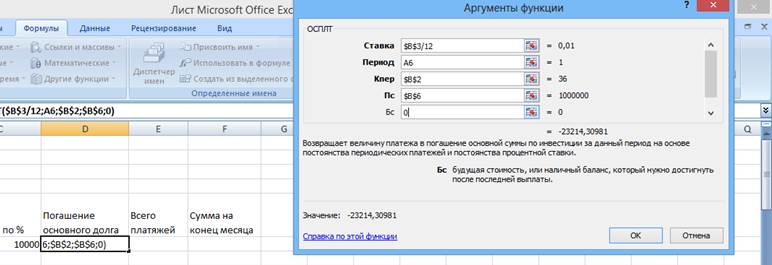
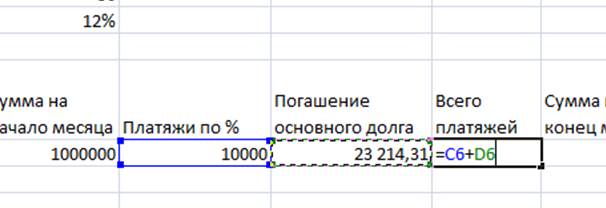
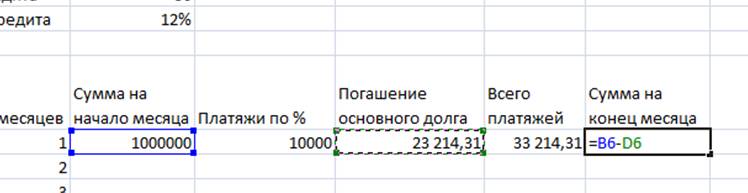
5. «Сумма на конец» =  «Сумма на начало»  - «Погашения основного долга». Делаем их относительными ссылками, растягиваем формулу до конца таблицы.

6. Заполняем таблицу полностью, и построить график.

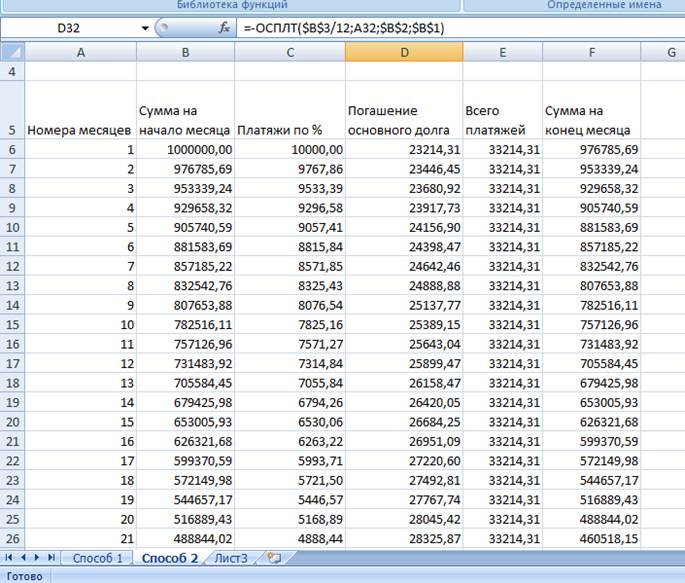
Способ 3

Третий способ - расчет будет производиться с помощью стандартной финансовой функции ПЛТ. ПЛТ - возвращает величину выплаты за один период годовой ренты.

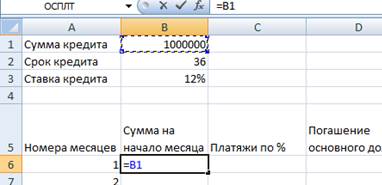
1. Сумма на начало месяца в первой ячейке – начальная сумма кредита, делаем ее постоянной ссылкой.

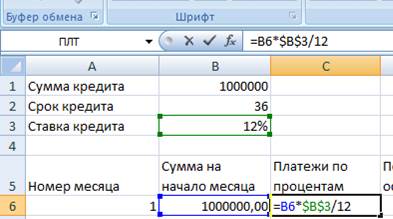
2. . «Платежей по %» = «сумма на начало» * «Годовая ставка кредита»/12. При этом «сумма на начало»  делаем переменной ссылкой,  т.к. она будет меняться от месяца к месяцу, а «Годовая ставка кредита» делаем постоянной ссылкой.

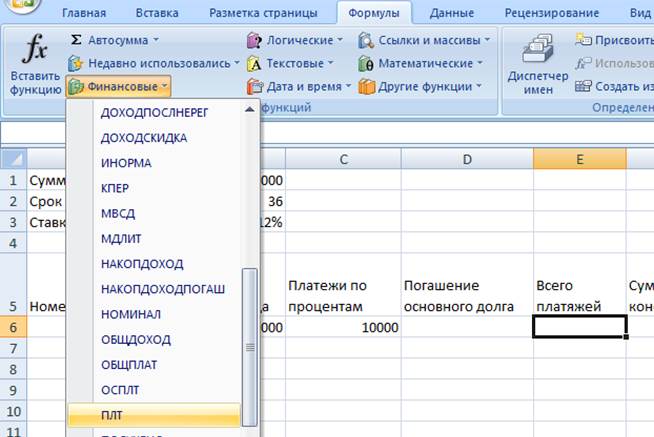
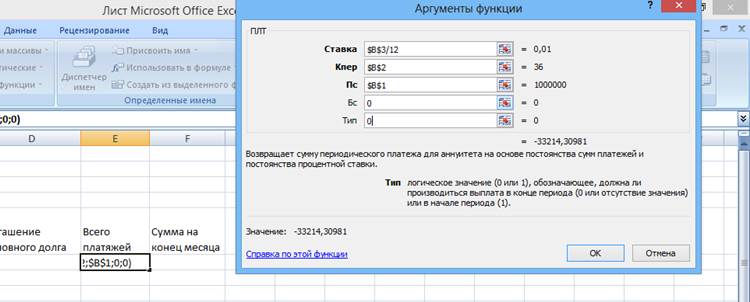
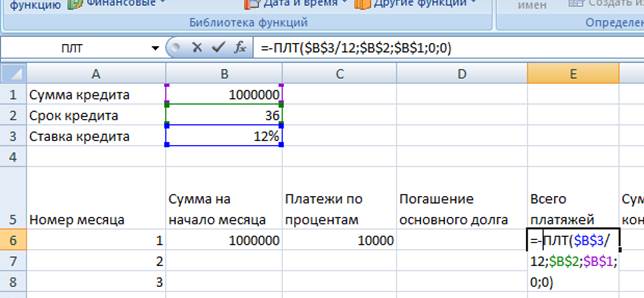
3. «Погашение основного долга» = «Всего платежей» - «Платежи по процентам»

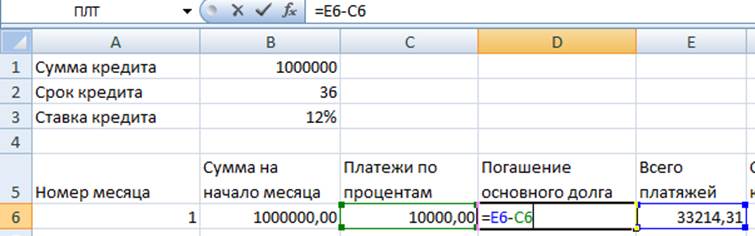
4. «Сумма на конец» =  «Сумма на начало»  - «Погашения основного долга». Делаем их относительными ссылками.

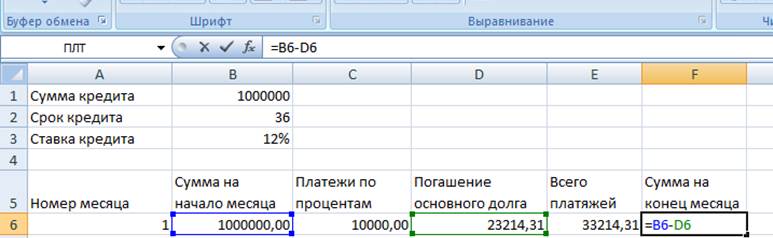
5.  Заполняем таблицу полностью, и построить график.

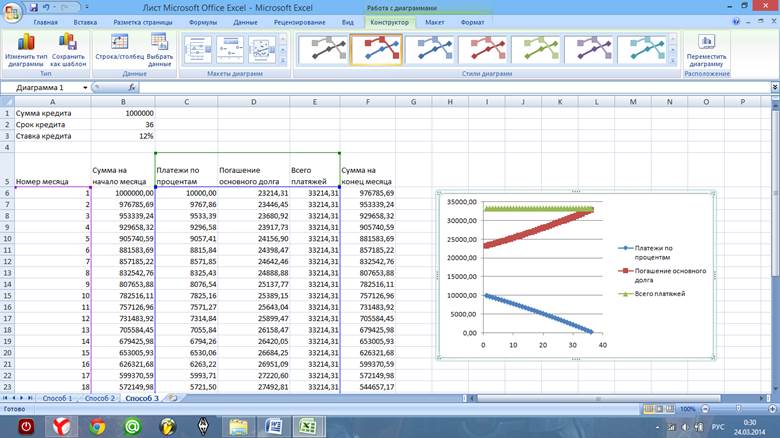
6. В итоге получаем таблицу со значениями, совпадающими с предыдущей таблицей расчета аннуитетного кредита.

Вывод: В ходе лабораторной работы научились рассчитывать доли платежей погашения основного долга и % по кредиту в месяц для дифференцированных и аннуитетных платежей, также научились рассчитывать с помощью финансовых функций ОСПЛТ, ПЛТ.