Моделирование транспортных процессов: Учебно-методический комплекс (Содержание дисциплины. Методические рекомендации по изучению дисциплины)

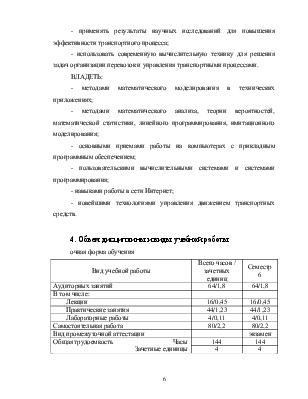
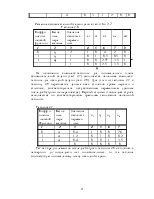
технологий, запасах ресурсов и стоимости восстановления приведены в таб. 2.3.

Таблица 2.3

╔══════════════════╦══════════════════════════════════╤═════╗

║    Тип ресурса   ║ Расход на один дв. по технологии │Запас║

║                  ╟────────┬────────┬────────┬───────┤     ║

║                  ║   1    │    2   │    3   │    4  │     ║

╠══════════════════╬════════╪════════╪════════╪═══════╪═════╣

║Электроэн.(квт.час║  100   │   130  │   90   │  110  │20000║

╟──────────────────╫────────┼────────┼────────┼───────┼─────╢

║Трудозатр.(чел.час║   50   │    30  │   70   │   45  │10000║

╠══════════════════╬════════╪════════╪════════╪═══════╪═════╣

║Стоимость (руб)   ║ 8000   │  7000  │ 8500   │ 7500  │     ║

╚══════════════════╩════════╧════════╧════════╧═══════╧═════╝

╔════╗200т         ┌──┐200т                 ╔════╗350т

║ А  ╟─────────────┤В ├─────────────────────╢ А  ║

║  1 ║      20км   │ 2│        25км         ║  3 ╟───┐

╚═╤══╝             └┬─┘                     ╚╤═══╝   │

│                 │                  ┌─────┘       │ 15км 

│10км             └──────┐           │             └┐

│                        │           │ 14км        ┌┴─┐300т

│                        │ 8км       │             │В │

┌┴─┐100т                  └┐     ┌────┘             │ 4│

│В │                       │     │                  └┬─┘

│ 1├───────────────────────┼─────┘               20км│

└─┬┘        18км           │                         │

│                        │ 20км                   ┌┴─┐250т

│ 12км                   │             ┌──────────┤В │

│                    ╔═══╧╗            │          │ 3│

└─────┐              ║ А  ║200т    16км│          └──┘

│           ┌──╢  2 ╟────────────┘

└───────────┘  ╚════╝

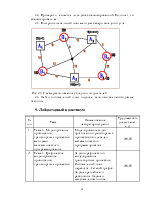
Рис.2.1. Схема расположения складов и получателей

Построить математическую модель,  анализ которой позволил бы  решить задачу о том,  для восстановления скольких двигателей следует использовать каждую из технологий с тем,  чтобы а) суммарные расходы на  их восстановление были бы минимальными, б) общее число восстановленных двигателей было бы максимальным.

Пример 4. Построить математическую модель в форме задачи математического программирования, используя следующие данные:

дислокация складов с имеющимися запасами материальных  средств  и получателей  с  их  потребностью  в материальных средствах показана на схеме (рис.2.1). Найти оптимальный по расходам в тонно-километрах план подвоза материальных средств со складов получателям.

Практическое занятие 2.2

Решение задач линейного программирования

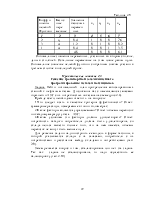
Пример 1. Решить геометрически задачу:  при строительстве автомобильной дороги принято решение о том, что дорожную одежду можно устраивать двумя способами,  которые отличаются друг от друга количеством и видами  расходуемых  материалов.  Так как общий вес расходуемых на один погонный метр дорожной одежды в обоих случаях примерно одинаков и равен шести тоннам,  то  приведем  процентный состав покрытий (таб. 2.4). В этой же таблице указаны объемы расходуемых материалов,  имеющиеся в наличии и стоимость одного погонного метра покрытия.

Таблица 2.4

╔══════════════╦═══════╤════════╤═════════╤═══════╦

║Показатели    ║ Песок │ Щебень │ Асфальт │ Бетон ║

╠══════════════╬═══════╪════════╪═════════╪═══════╬

║1-й способ,(%)║   50  │   30   │   10    │  10   ║

╟──────────────╫───────┼────────┼─────────┼───────╫

║2-й способ,(%)║   40  │   45   │   15    │   0   ║

╟──────────────╫───────┼────────┼─────────┼───────╫

║Всего в нали- ║  120  │  108   │   36    │  12   ║

║чии, тыс.т    ║       │        │         │       ║

╚══════════════╩═══════╧════════╧═════════╧═══════╩

Построить математическую модель для определения того,  сколько погонных метров дорожного покрытия следует устроить каждым из  способов, чтобы суммарная длина покрытия была максимальной.

Математическая модель этой задачи имеет вид:

Здесь  - длина покрытия, устроенного первым способом;  - вторым. Для удобства построения графиков  и  измеряются в десятках километров.

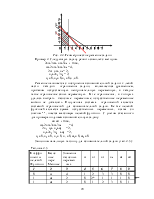
Для геометрического решения надо построить множество допустимых планов и линию уровня l целевой функции. Сдвигая эту линию в направлении возрастания значений целевой функции как можно дальше, но так, чтобы она пересекала множество допустимых планов, получим прямую L, которая пересекает множество допустимых планов в точке P. Эта точка соответствует оптимальному плану задачи (см. рис.2.2).

Так как точка P лежит на пересечении прямых

  и  

то ее координаты есть =1.714 и =2.857. Значит, общая протяженность дороги равна 1.714+2.857=4.571 десятков километров или 45710 метров.

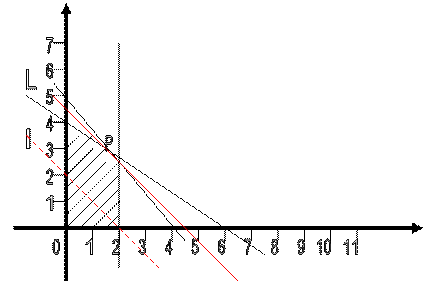
Рис. 2.2. Геометрическое решение задачи

Пример 2. Следующую задачу решить симплекс-методом.

2x₁+3x₂+ x₃+5x₄ max,

x₁+2x₂+3x₃+3x₄ = 4,

2x₂- x₃+ x₄ = 2,              

x₂+2x₃-3x₄ = 2,

x0,x0,x0,x0.

Решение начинается с построения вспомогательной задачи: к левой  части  каждого  ограничения задачи,  являющегося уравнением, прибавим искусственную неотрицательную переменную, в каждое такое ограничение свою переменную.  В те ограничения,  в которых удалось выбрать  базисные  переменные, искусственные переменные можно не добавлять. Полученная система  ограничений является системой ограничений для вспомогательной задачи. Ее же целевой функцией является сумма  искусственных  переменных,  взятая  со знаком "-", ищется максимум целевой функции.  С учетом сказанного для примера получаем вспомогательную задачу:

-u₁-u₂max,

x₁+2x₂+3x₃+3x₄         =4,

2x₂- x₃+ x₄+u₁         =2,             

x₂+2x₃-3x₄   +u₂     =2,

x0, x0, x0, x0, u0, u0.

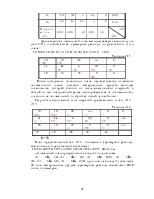
Заполним начальную таблицу для вспомогательной задачи (таб. 2.5):

Таблица 2.5

Решение вспомогательной задачи дано в таб. 2.6 и 2.7.                              

Таблица 2.6

На основании симплекс-таблицы для оптимального плана вспомогательной задачи (таб. 2.7) заполняется начальная симплекс-таблица для исходной задачи (таб. 2.8). Для этого из таблицы 2.7 в таблицу 2.8 переносятся данные всех столбцов кроме первого и столбцов, соответствующих искусственным переменным (данные последней строки не переносятся). Первый столбец и последняя строка заполняются по соответствующим правилам заполнения начальной таблицы.

Таблица 2.7

Так как среди элементов последней строки таблицы 2.8 в столбцах с четвертого до последнего нет положительных, то эта таблица соответствует оптимальному плану исходной задачи.

  Таблица 2.8

Оптимальные значения переменных, указанных во втором столбце, даны в столбце 3. Остальные переменные на этом плане равны нулю. Оптимальное значение целевой функции с обратным знаком указано в третьем столбце в последней строке.

Практическое занятие 2.3

Решение транспортной задачи линейного

программирования методом потенциалов

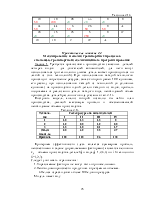
Задача. Найти  оптимальный  план прикрепления автозаправочных станций к нефтяным базам.  Дислокация баз с имеющимися запасами горючего и АЗС с их  потребностью показана на схеме (рис.2.3).

Прежде всего, необходимо ответить  на  вопросы: 

1.Что следует взять в качестве критерия эффективности? Ответ: суммарные расходы, измеряемые в тонно-километрах;

2.Какие факторы являются управляемыми? Ответ: объемы перевозок по каждому маршруту база – АЗС;

3.Каким условиям эти факторы должны удовлетворять? Ответ: потребность каждого потребителя должна быть удовлетворена, со склада нельзя вывезти больше того, что на нем имеется, объемы перевозок не могут быть меньше нуля.

Для решения задачи надо построить ее модель в форме таблицы