Моделирование объектов систем компьютерного управления; сбор и фиксация результатов моделирования. Вариант № 4, страница 2

Рис. 10. Фазовый портрет

2) х0 = 0, с=2В

а) a1=a1биф

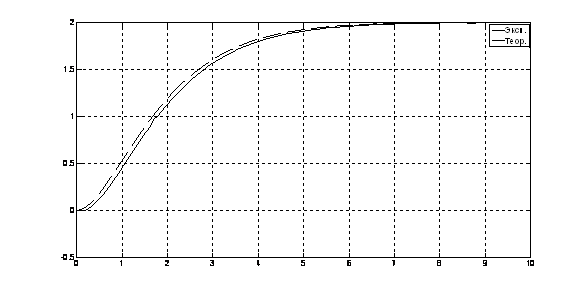
Рис. 11. Переходный процесс х(t) = f1(t)

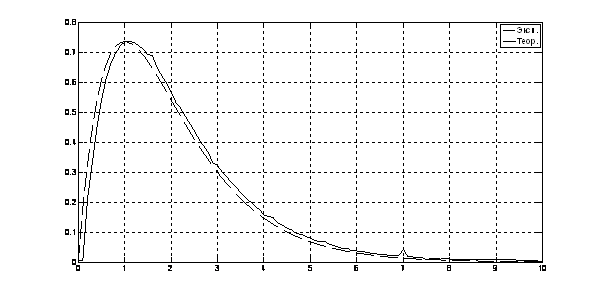
Рис. 12. Переходный процесс  (t) = f2(t)

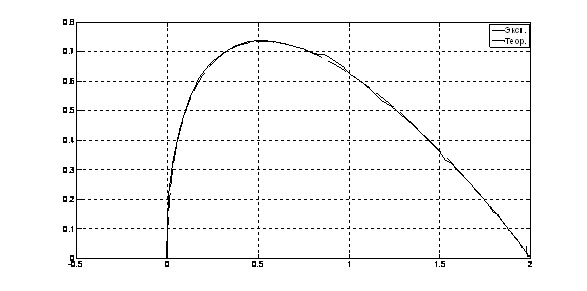
Рис. 13. Фазовый портрет

б) a1=0.5*a1биф

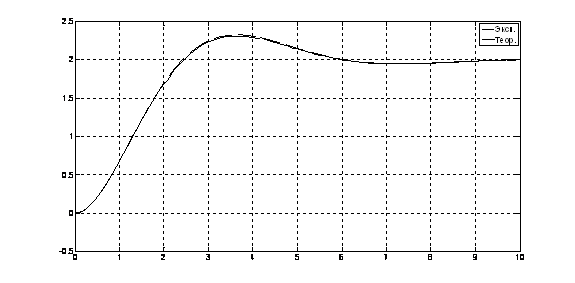
Рис. 14. Переходный процесс х(t) = f1(t)

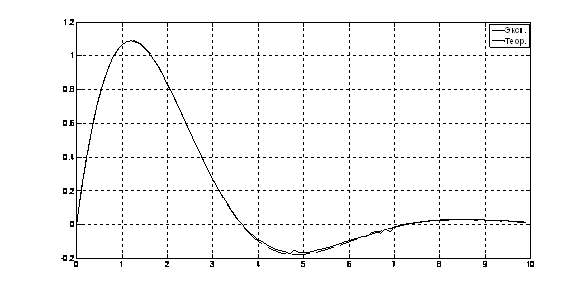
Рис. 15. Переходный процесс  (t) = f2(t)

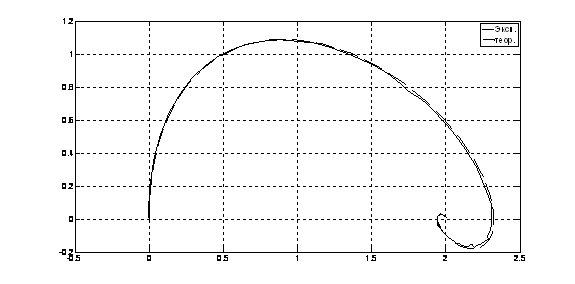
Рис. 16. Фазовый портрет

в) a1=2*a1биф

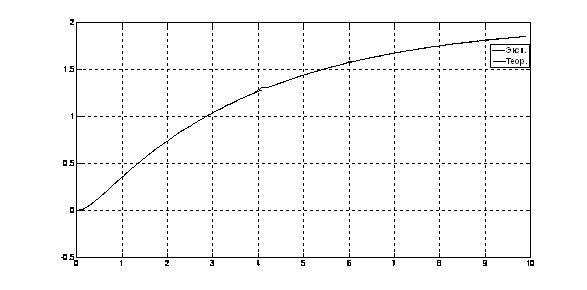
Рис. 17. Переходный процесс х(t) = f1(t)

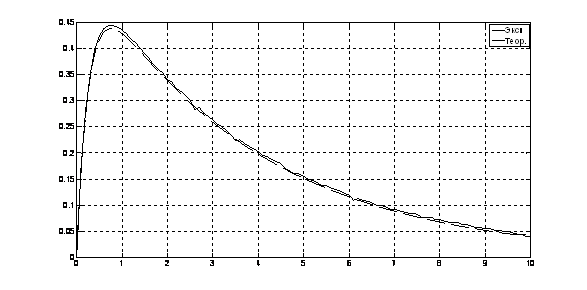
Рис. 18. Переходный процесс  (t) = f2(t)

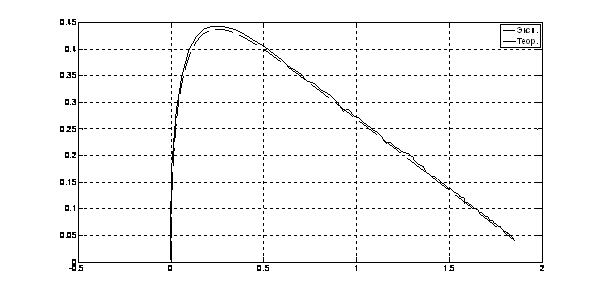
Рис. 19. Фазовый портрет

2) Автоколебания (α1=0)

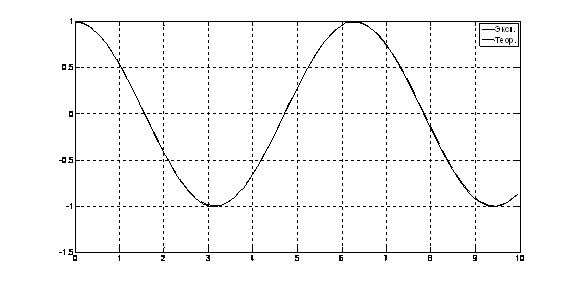
Рис. 20. Переходный процесс х(t) = f1(t)

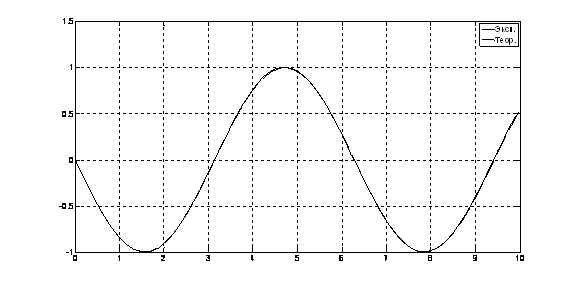
Рис. 21. Переходный процесс  (t) = f2(t)

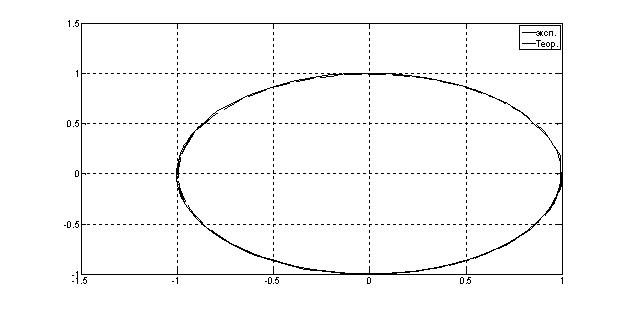
Рис. 22. Фазовый портрет

Оценка относительной погрешности моделирования на АВК-31:

. Далее приведены средние значения относительных погрешностей всех зависимостей.

1) х0 = 2В, с=0

а) a1=a1биф

=0.89%, =0.78%

б) a1=0.5*a1биф

 = 0.50%, =0.60%

в) a1=2*a1биф

 =0.65%, = 1.16%

2) х0 = 0, с=2В

а) a1=a1биф

 =1.21,  =1.69%

б) a1=0.5*a1биф

 =0.37%, = 0.54%

в) a1=2*a1биф

= 0.11%, =0.95%

2) Автоколебания (α1=0)

Расчет частоты автоколебаний:

Анализ результатов и выводы:

Полученные в процессе работы экспериментальные зависимости имеют среднюю относительную погрешность не более 1.3%, что характерно для АВК – их точность не высока. В результате работы можно сделать вывод о сложности использования АВК в связи с необходимостью решения уравнений для определения коэффициентов подобия. К преимуществам использования данного метода относится решение ДУ процесса в темпе процесса.