µ=µ0•eιωt
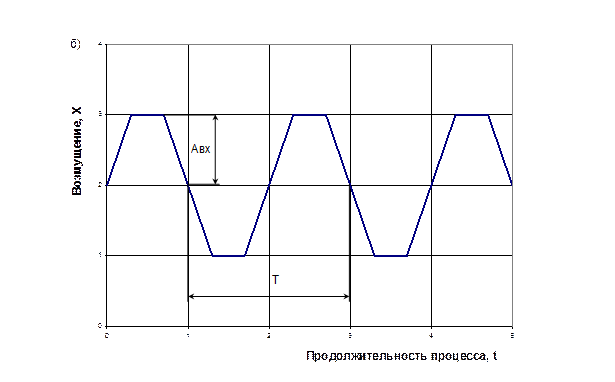
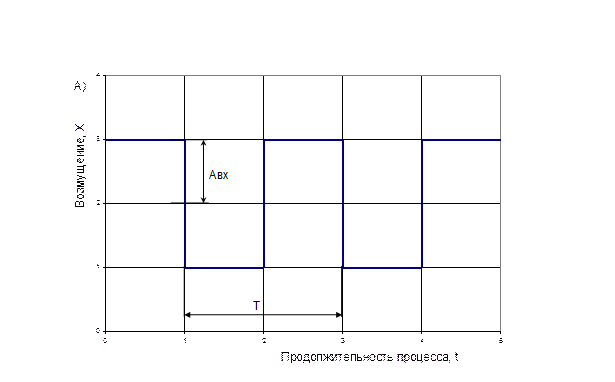
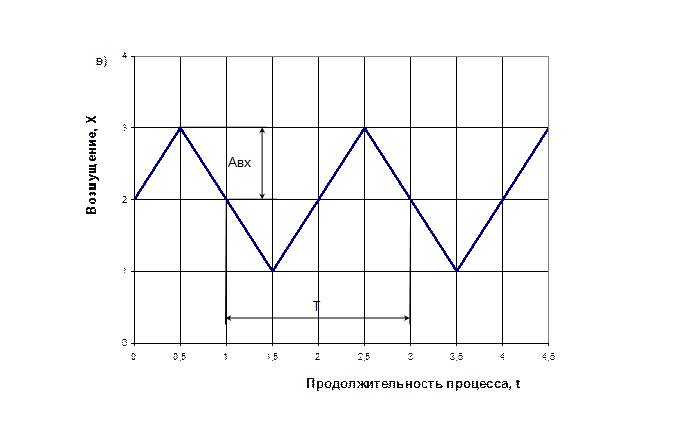
Реакция звена на гармоническое возмущение зависят от частотных характеристик. Последние определяются проведением ряда экспериментов при гармоничном изменении входной координаты с различными частотами. Для этого на вход объекта путем перестановки регулирующего органа подаются периодические колебания X типа прямоугольной волны, трапецеидальной или треугольной формы (рисунок 1)
Основными характеристиками гармонических возмущении являются амплитуда Авх, период Т и частота ω , определяемая по формуле
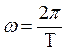 (1)
(1)
Испытаний начинаются на низких частотах ωL. Затем они повышается до наступления момента, когда колебания входной координаты Х полностью поглощаются объектом. На выходе при этом не обнаруживаются периодические изменения выходная величины Y. Частота возмущающего воздействия, при которой в объекте автоматического регулирования не происходит изменения выходной координаты, называется частотой среза ωср.
Экспериментальное определение значения частоты среза важно по той причине, что оно характеризует динамические свойства объекта. Чем он инерционнее, тем меньше ωср . Следует учитывать, что значение ωср при экспериментальном определении зависит не только от свойств объекта, но и от прибора, измерявшего выходную координату: чем выше чувствительность последнего, тем больше ωср.
Для получения частотных характеристик объекта проводят эксперименты для 8-1O значений периода колебаний Tвходной величины. При этом обязательным условием начала каждого опыта является установившийся режим работы объекта. Измерения амплитуды Авых и фазы φвых выходных колебаний производят после окончания переходного процесса (примерно через 2 периода Т), поскольку вначале колебания выходной величины отличаются от синусоидальных за счет свободных составлявших, которые впоследствии затухают.
Отношение выходной величины АС к входной, выраженное в комплексной форме, называется амплитудно-фазовой характеристикой автоматической системы.
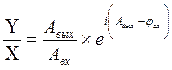 ,
,
Амплитудно-фазовая характеристика не завидит от времени. В этом ее отличие от временной, характеристики. Следовательно, если временная характеристика ( например, кривая разгона ) определяет поведение системы в переходном процессе, то амплитудно-фазовая характеристика выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах.
 |
 |
||||
 |
|||||
Отношение
амплитуды ![]() является модулем амплитудно-фазовой
характеристики и называется амплитудно-частотной характеристикой системы
является модулем амплитудно-фазовой
характеристики и называется амплитудно-частотной характеристикой системы
![]() W(ω)=
W(ω)=![]() ,
,
Разность фаз выходной и входной φвх величин является фазой амплитудно-фазовой характеристики и называется фазо - частотной характеристикой системы
φ(ω)=φвых-φвх
Частота, на которой проводится эксперимент, определяется по формуле (1)
Фазо-частотная характеристика φ(ω) может быть определена из экспериментально снятых кривых (рис.2.) формуле
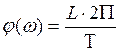 , (7)
, (7)
где L - расстояние между точками кривых изменения входной и выходной величин, находящимися в одной фазе.L принимается со знаком "+", если выходные колебания опережает входные. В противном случае - со знаком "-". Для правильного определения L нужно отсчитать одинаковое число периодов от начала эксперимента и измерить расстояние между однофазными точками вынуждающих и вынужденных колебаний.
При применении возмущающих колебаний типа прямоугольной волны их можно рассматривать как сумму синусоидальных колебаний различных частот и амплитуд. Проходя через объект, каждая из этих гармоник вызовет на выходе колебания той же частоты, но отличающиеся фазой и амплитудой.
Для прямоугольных колебаний входной величины амплитуда гармонического возмущения определяется из выражения
Авхi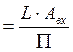 ,
,
Амплитуду первой гармоники выходных колебаний и сдвиг по фазе этой амплитуды относительно первой амплитуды входных, колебаний находят по формулам
![]() ,
,
Значения a1 и b1 определяют по методу "двенадцати ординат". Для этого период T делят на 12 равных частей и каждому отрезку находят соответствующее значение Xi. Полученные данные подставляет в формулы
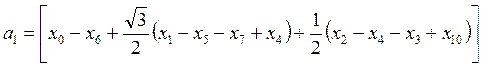 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.