Правило преобразования структурных схем

выходная величина каждого предшествующего звена является входным воздействием последующего звена. При преобразовании структурных схем

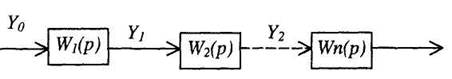
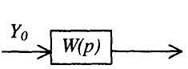
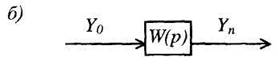
Рис. 3. Преобразование последовательно соединенных звеньев цепочку из последовательно соединенных звеньев можно заменить одним звеном (рис. 3 б) с передаточной функцией W(p), равной произведению передаточных функций отдельных звеньев:

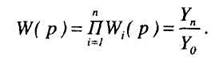
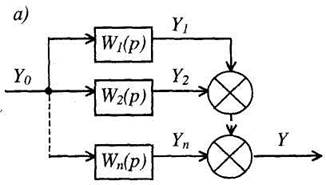
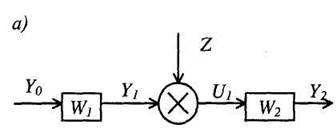
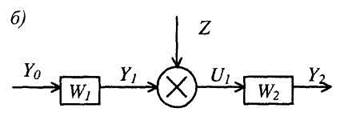
2. Параллельное соединение звеньев. При параллельном соединении (рис. 4, а) на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь из параллельно соединенных звеньев можно заменить одним звеном (рис. 4, б) с передаточной функцией W(p), равной сумме передаточных функций входящих в нее звеньев:

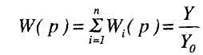
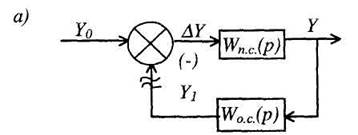
3. Звено, охваченное обратной связью. Принято считать, что звено охвачено обратной связью (рис. 5, а), если его выходной сигнал через какое-либо другое звено подается на вход. При этом обратная связь считается отрицательной, если сигнал y₁ вычитается из входного сигнала у_о ,т.е.

Обратная связь считается положительной, если сигнал y₁ складывается с входным сигналом у_о, т.е.

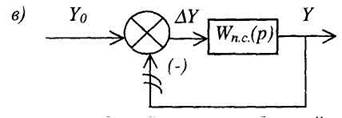
Разомкнем обратную связь перед сравнивающим звеном (рис. 2.15, а). Тогда получим цепь из двух последовательно соединенных звеньев. Передаточная функция разомкнутой цепи будет равна произведению передаточной функции Wn.c. прямой цепи и передаточной функции W₀.c. обратной связи:

Рис. 4. Преобразование параллельно соединенных звеньев

Рис. 5. Преобразование обратной связи

Передаточная функция W_з(p) замкнутой цепи с отрицательной обратной связью, равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи:

Передаточная функция замкнутой цепи с положительной обратной связью равна передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи:

Если передаточная функция W₀.c.(p) = 1, то обратная связь называется единичной и структурная схема изображается, как показано на рис. 5, в. Передаточная функция при этом принимает вид:

при отрицательной обратной связи

при положительной обратной связи

При преобразовании структурных схем возникает необходимость переноса и перестановки сумматоров и узлов. Рассмотрим, какие изменения в схеме при этом нужно произвести.

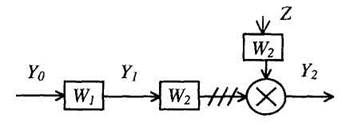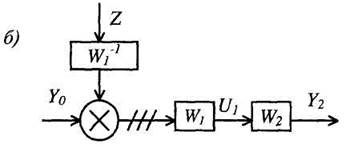
Рис. 6. Перенос сумматора через звено: а - влево; б - вправо

4.  Правило переноса сумматора. Легко показать, что при переносе сумматора (рис. 6) по ходу сигнала необходимо добавить звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор (рис. 6, а). Если сумматор переносится против хода сигнала, то необходимо добавить звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор (рис. 6, б).

При переносе сумматора возникают неэквивалентные участки линии связи. Эти участки на рис. 6 заштрихованы.

5. Перенос узла. При переносе узла (рис. 7, а) также необходимо добавить звено. Если узел переносится по ходу сигнала, то добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел

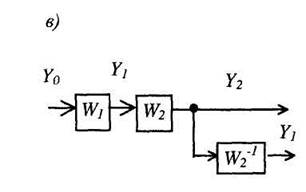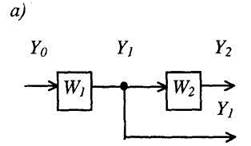
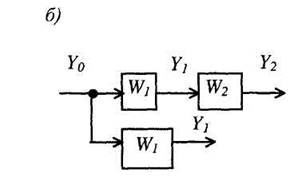
Рис. 7. Перенос узла

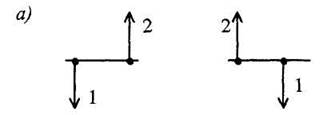
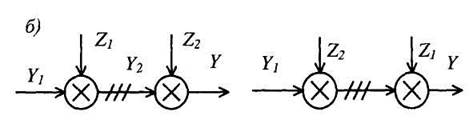
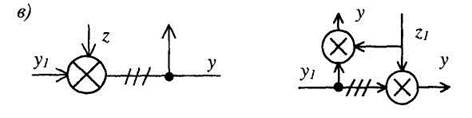
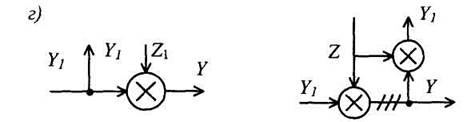
Рис. 8. Перенос узлов и сумматоров

(рис. 7, б). Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел (рис. 7, в).

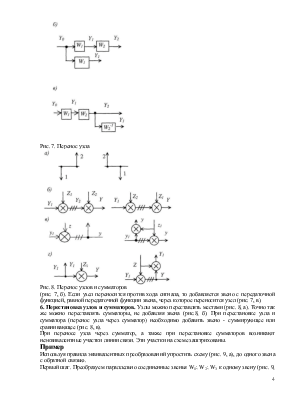
6. Перестановка узлов и сумматоров. Узлы можно переставлять местами (рис. 8, а). Точно так же можно переставлять сумматоры, не добавляя звена (рис.8, б). При перестановке узла и сумматора (перенос узла через сумматор) необходимо добавить звено - суммирующее или сравнивающее (рис. 8, в).

При переносе узла через сумматор, а также при перестановке сумматоров возникают неэквивалентные участки линии связи. Эти участки на схеме заштрихованы.

Пример

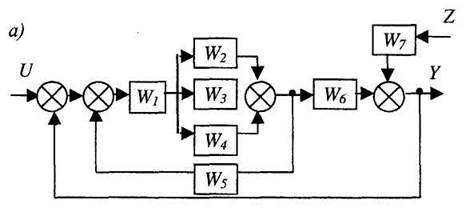
Используя правила эквивалентных преобразований упростить схему (рис. 9, а), до одного звена с обратной связью.

Первый шаг. Преобразуем параллельно соединенные звенья W₁; W₂; W₃ к одному звену (рис. 9, б) с передаточной функцией: W₈ = W₂ + W₃ + W₄.

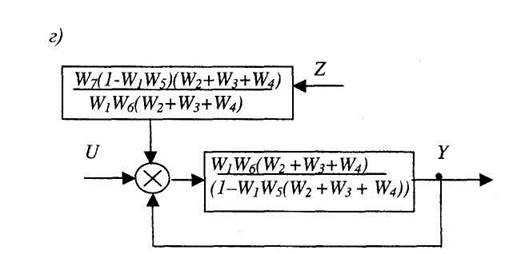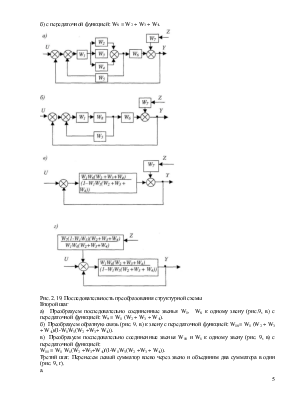
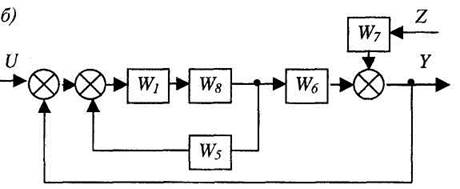
Рис. 2.19. Последовательность преобразования структурной схемы

Второй шаг а)  Преобразуем последовательно соединенные звенья W₁,  W₈ к одному звену (рис.9, в) с передаточной функцией: W₉ = W₁ (W₂ + W₃ + W₄).

б)  Преобразуем обратную связь (рис. 9, в) к звену с передаточной функцией: W₁₀= W₁ (W₂ + W₃ + W₄)/(l-W₁W₅(W₂ +W₃+ W₄)).

в)  Преобразуем последовательно соединенные звенья W₁₀ и W₆ к одному звену (рис. 9, в) с передаточной функцией:

W₁₁ = W₁ W₆(W₂ +W₃+W₄)/(l-W₁W₅(W₂ +W₃ + W₄)).

Третий шаг. Перенесем левый сумматор влево через звено и объединим два сумматора