Анализ электрического состояния линейных однофазных электрических цепей синусоидального тока

Министерство образования Российской Федерации

Комсомольский-на-Амуре Государственный Технический Университет

Кафедра “Электротехники”

Расчётно-Графическое Задание № 2

«Анализ электрического состояния линейных однофазных электрических цепей синусоидального тока»

Вариант №11

Группа: 8ТЭ

Студент: Логунов А.А.

Преподаватель: Крупский Р.Ф.

Комсомольск-на-Амуре  2000.

Задание

На рис. 1 представлена схема замещения однофазной электрической цепи синусоидального тока. Со смешанным соединением элементов. Параметры элементов ветвей цепи равны:

R₁= 6 Oм, C₁= 199 мкФ, R₂= 12 Oм, L₂= 9,55 мГн, C₂= 106.16 мкФ, R₃= 20 Oм, C₃= 106.16 мкФ.

Задаётся уравнение для мгновенных значений тока

i₁=28.2sin(628t - 45)

Определить

1)  действующие значения токов ветвей и напряжений на зажимах ветвей и цепи;

2)  активные, реактивные и полные мощности ветвей и цепи.

Написать уравнения для мгновенных значений токов ветвей, напряжений на зажимах ветвей и цепи.

Составить баланс активных и реактивных мощностей цепи.

Построить в масштабе векторную диаграмму цепи.

Задачу решить символическим (комплексным) методом.

Схема замещения однофазной электрической цепи синусоидального тока.

Анализ

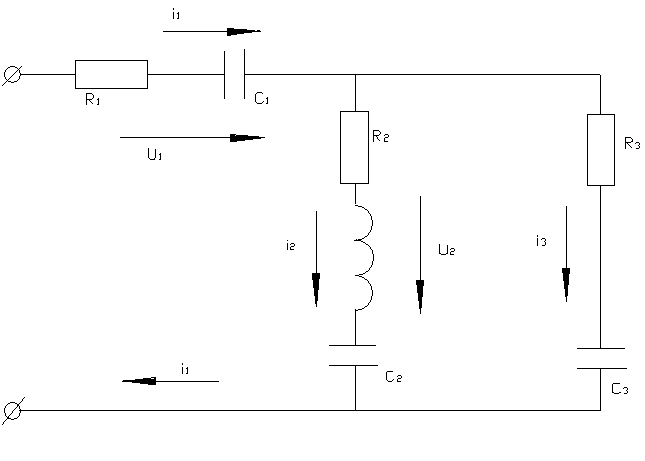
1) Определим действующие значения токов ветвей и напряжений на зажимах ветвей и цепи. Решение:

Вычислим реактивные сопротивления ветвей:

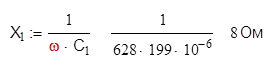
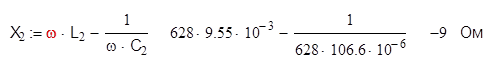
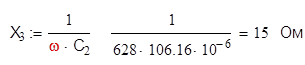
Вычислим комплексные сопротивления ветвей и цепи

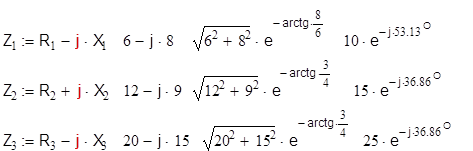
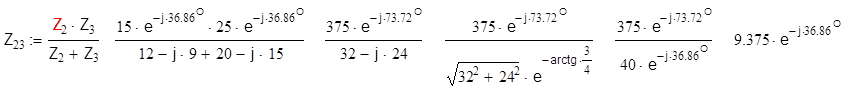
Вычислим действующее значение силы тока:

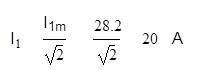
Затем вычислим действующие значения  токов и напряжений остальных ветвей цепи:

 

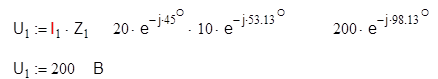
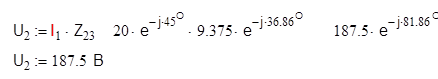
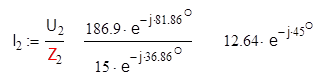
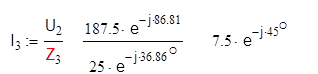
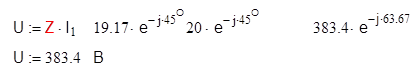
2) Определим уравнения для мгновенных значениях токов ветвей и напряжений на зажимах ветвей и цепи

Решение:

Уравнения для мгновенных значений тока и напряжения имеют вид:

i=I_msin(wt +y_i );  u=U_msin(wt +y_u ), где w-угловая частота синусоидальных колебаний тока и напряжения.

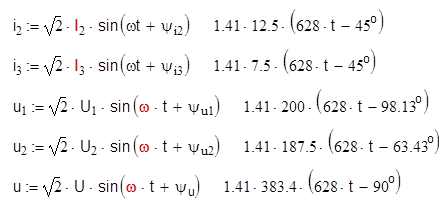
3) Определим активные, реактивные и полные мощности ветвей и цепи.

Решение:

Вычисление комплексной мощности позволяет одновременно определить активную и реактивную мощности

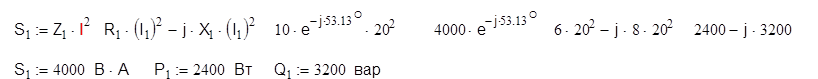
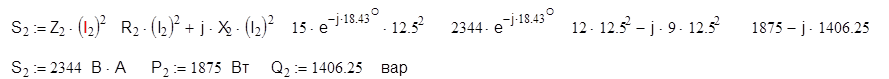
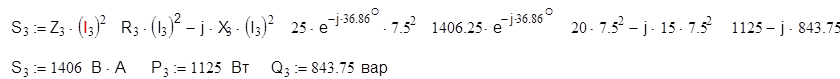
4) Определим баланс активных и реактивных мощностей.

Решение:

Для проверки правильности проведённых расчётов составим уравнения баланса активных и реактивных мощностей:

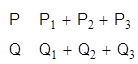
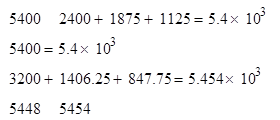
Выполнение баланса активных и реактивных мощностей подтверждает правильность наших расчётов.

5) Построим векторную диаграмму цепи.

Составим уравнения для построения векторной диаграммы цепи:

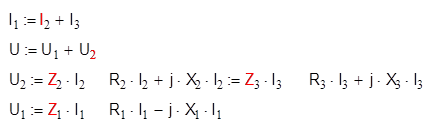
Вычислим активные и реактивные составляющие напряжений на  элементах ветвей

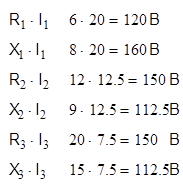
Для построения векторной диаграммы на комплексной плоскости выберем масштабы для токов и напряжений:

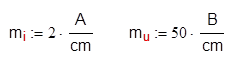
На основании произведённого анализа цепи, представленной на рисунке, построим векторы токов i₁,

i₂, i₃, а затем векторы активных и реактивных составляющих напряжений на  элементах ветвей.

Векторная диаграмма цепи

 

Анализ векторной диаграммы цепи подтверждает ранее сделанное заключение о том, что расчёт цепи произведён правильно.