Использование функции Подбор параметра (Solve For) в электронных таблицах. Моделирование статистических данных в электронных таблицах Excel

2. Использование  функции Подбор параметра (Solve For) в ЭТ

В экономической практике весьма часто возникает задача найти необходимое, часто предельное, значение рассчитанного значения функции в зависимости от изменения какого-нибудь параметра, влияющего на результат. Для этого в ЭТ широко используются специальные функции подбора параметра.

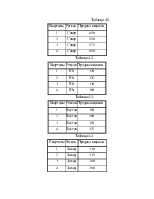
Рассмотрим пример. Пусть  в инвестиционном комплексе рассчитан Внутренний Уровень Доходности (ВУД). По его рассмотрении выясняется, что доходность слишком низка - 9%. Как поднять ее до 20%, например, за счет снижения инвестиций. Исходные данные приведены в форме1.

Форма 2. 1.

2.1 Использование  функции Solve For в Quattro Pro For Windows

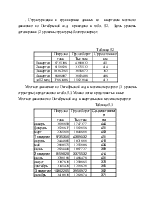
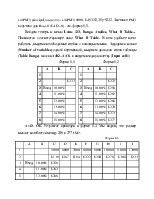
Откроем QPW. Создадим таблицу по аналогии с формой1. В ячейку С2 введем функцию IRR (ВУД). Для этого войдем в режим редактирования С2, появляется кнопка @- функций, щелкнем по ней, войдем в список функций, найдем финансовые Financial, а в них  потоковые денежные (CashFlow), и далее IRR. @IRR(0,B2..B6)=9%. Войдем в меню QPW, Tools, Solve For. Выводится окно SolveFor, в нем в поле FormulaCell  указываем клетку С2. В поле TargetValue -значение цели укажем 20%, посредством клетки с переменной (VariableCell)- B2.

Форма2.2

Установим максимум итераций (MaxIterations)-25 и требуемую точность (Accuracy) - 0.0005. OK . Результат приведен  в форме 2.

2.2 Использование  функции Solve For в Lotus 123

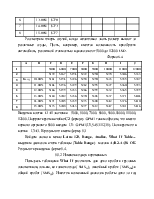
Откроем Lotus 123. Создадим таблицу по аналогии с формой 1. В ячейку С2 введем функцию IRR (ВУД). Для этого щелкнем по кнопке @, войдем в список функций - ListAll, найдем финансовые Financial, а в них IRR. @IRR(0,B2..B6)=9%. Войдем в меню Lotus 123, Range, Analyze, Backsolver. Выводится окно Backsolver, в нем в поле MakeCell  указываем клетку С2. В поле EqualtoValue -значение цели укажем 20%, посредством изменяемой клетки (Bychangingcell(s))- B2.OKВ результате имеем тот же результат, что и в форме 2.

3.Моделирование статистических данных в ЭТ Excel

3.1. Описательная статистика

Массивы экономических показателей характеризуются значениями средних величин различного вида, вариацией ряда, моментами распределения (начальные, центральные) и законами распределения.

Статистика различает два вида моментов случайной величины определенной степени:

Þ  начальный — математическое ожидание случайной величины — m_k

Þ  центральный — математическое ожидание отклонения случайной величины от математического ожидания  — M_k

В описательной статистике применяются следующие показатели значений случайной величины:

Þ  средняя арифметическая — начальный момент первого порядка, математическое ожидание значений случайной величины при большом числе испытаний — x_cp

Þ  средняя квадратическая — начальный момент второго порядка— x_cp2,

Þ  средняя кубическая — начальный моменттретьего порядка —x_cp3,.

Þ   средняя геометрическая для оценки средних темпов роста случайных величин, нахождения значения признака, равноудаленного от минимального и максимального значения — x_cpгеом.

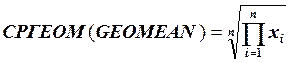
GEOMEAN(4;5;8;7;11;4;3) =5,476987

Þ  средняя гармоническая для определения средней суммы обратных величин — x_cpгарм.

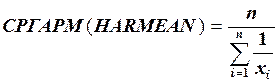
Примем: B1=1; B2=3; B3=3; B4=4; B5=5

HARMEAN(B1:B2)=1.5

HARMEAN(B1:B3)=1.8

HARMEAN(B2:B4)= 3.272727

HARMEAN(B1:B5)= 2.362205

Полезно знать, что между средними существует соотношение:

x_cpгарм. <= x_cpгеом<= x_cp<= x_cp2<=x_cp3

Для измерения рассеивания значений признака относительно математического ожидания используются другие показатели:

Þ   дисперсия — второй центральный момент, математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Различают дисперсию по выборке (ДИСП) и дисперсию по генеральной совокупности (ДИСПР)

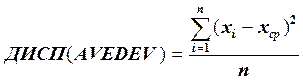
Þ  среднее квадратическое отклонение  (стандартное отклонение) — корень квадратный из дисперсии случайной величины. Различают стандартное отклонение  по выборке (СТАНДОТКЛОН) и стандартное отклонение  по генеральной совокупности (СТАНДОТКЛОНП).

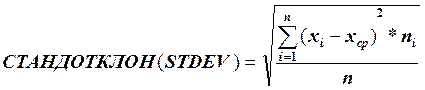
Þ  cредний модуль отклонения — среднее значение абсолютной величины разности случайной величины и средней.

Þ  максимум— максимальное значение данных ряда.

Þ  минимум—минимальное значениеданных ряда.

Þ  наибольшее — предшествующее максимуму значение.

Þ  наименьшее— следующее после минимума минимальное значение