Система автоматического регулирования скорости паровой турбины со статическим регулятором скорости непрямого действия, страница 2

Откуда находим

Δφ = 200 λ

Подставляя полученные выражения в уравнение (1), получим уравнение динамики объекта регулирования в безразмерных координатах.

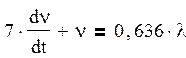
Применяя к полученному уравнению преобразование Лапласа, получим:

Передаточная функция объекта регулирования:

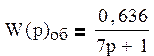
2.2 Уравнение динамики датчика скорости регулятора.

В общем случае динамика центробежного датчика скорости описывается апериодическим звеном 2-ого порядка, д.у. которого записывается в виде:

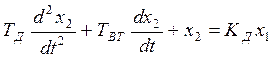                                                 (2)

где   Тд  = 1,25 [с]    -   постоянная времени датчика;

Твт = 0,5 [с]    -   время вязкого трения датчика;

Кд  =  0.8       -   коэффициент усиления датчика;

Х2   =   ΔS     -   приращение перемещения муфты датчика скорости;

Введём безразмерные координаты и новые переменные. Из пояснения к выводу уравнения динамики объекта регулирования берём:

         х₁ = Dwд = 1046,69ν

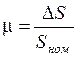   -  безразмерный ход муфты датчика скорости;

где = 20 [мм]   -   номинальный ход муфты (для всех вариантов);

ΔS  =  20μ

Подставляя полученные выражения в уравнение (2), получим уравнение динамики датчика скорости в безразмерных координатах.

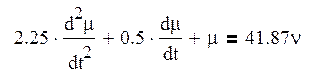
Применяя к полученному уравнению преобразование Лапласа, получим:

Передаточная функция датчика скорости:

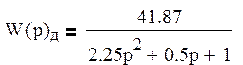
2.3 Уравнение динамики сервомеханизма.

Динамика сервомеханизма описывается типовым динамическим интегрирующим звеном, , д.у. которого записывается в виде:

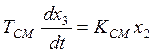                                                              (3)

где   Тсм  =  2 [с]  -   постоянная времени сервомеханизма РНД;

Ксм  =  5          -    коэффициент усиления сервомеханизма РНД;

х₂ = DS = 20m  -  приращение перемещения муфты датчика скорости;

х₃ =   -  приращение выходной координаты сервомеханизма, мм;

Подставляя полученные выражения в уравнение (3), получим уравнение динамики сервомеханизма в безразмерных координатах.

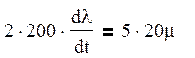
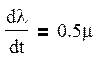
Применяя к полученному уравнению преобразование Лапласа, получим:

Передаточная функция сервомеханизма:

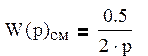
2.4 Уравнение динамики жесткой МООС.

В общем случае динамика гибкой МООС описывается типовым динамическим дифференцирующим звеном.

где      ξ = Δl  -  приращение выходной координаты МООС;

Введём относительные координаты выходного параметра МООС.

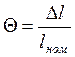     -    безразмерная выходная координата МООС;

= 25 [мм] - номинальное значение выходной координаты МООС (для всех вариантов);

х₃ =

Подставляя полученные выражения в уравнение (4), получим уравнение динамики жесткой МООС в безразмерных координатах.

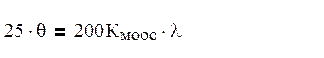
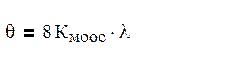
Передаточная функция жесткой МООС:

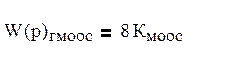
4. Исследование динамики САР с использованием системы MatLAB

h1=tf(0.636,[7 1])              % передаточная функция объекта регулирования

h2=tf(4.187,[2.25 0.5 1])   % передаточная функция датчика

h3=tf(0.5,[2 0])                  % передаточная функция сервомеханизма

h4=tf(0.4)                           % передаточная функция жесткой МООС

h5=feedback(h3,h4)           % передаточная функция с/механизма, охваченного жесткой МООС

h6=series(h2,h5)                % передаточная функция регулятора, охваченного жесткой МООС

h7=series(h6,h1)                % передаточная функция разомкнутой САР

poles(h7)

ans =

-0.1111 + 0.6573i

-0.1111 - 0.6573i

-0.1429         

-0.1000         

k1=dcgain(h7)                        %коэффициент передачи разомкнутой системы

k1=6,65

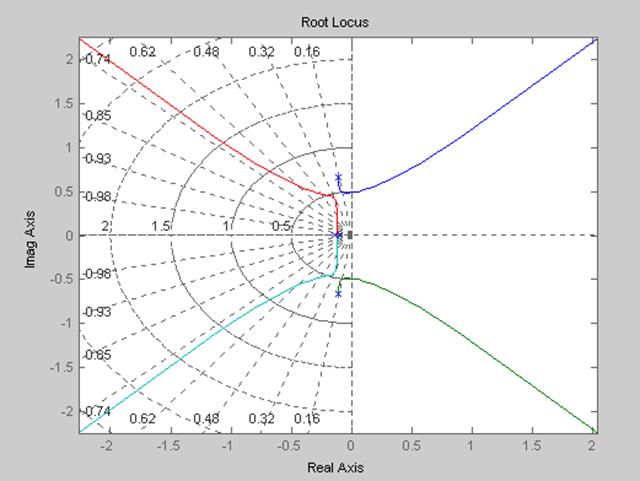
rlocus(h7), sgrid                     %построение корневого годографа

k2=rlocfind(h7)                      %интерактивный съем информации с гр. корн. годографа

h8=series(h7,k1/k2)               %передаточная функция разомкнутой системы с Kopt

k3=dcgain(h6)                        %коэффициент передачи регулятора

k3=10,46

k4=dcgain(h1)                        %коэффициент передачи объекта

h9=series(h6,k2/k3*k4)         %передаточная функция регулятора с Kopt

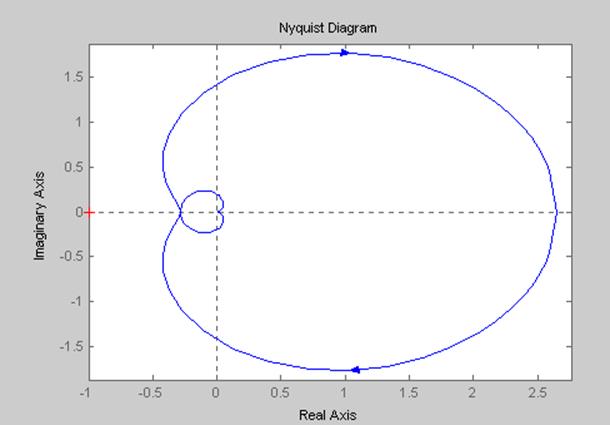
nyquist(h8),grid                      %годограф Найквиста

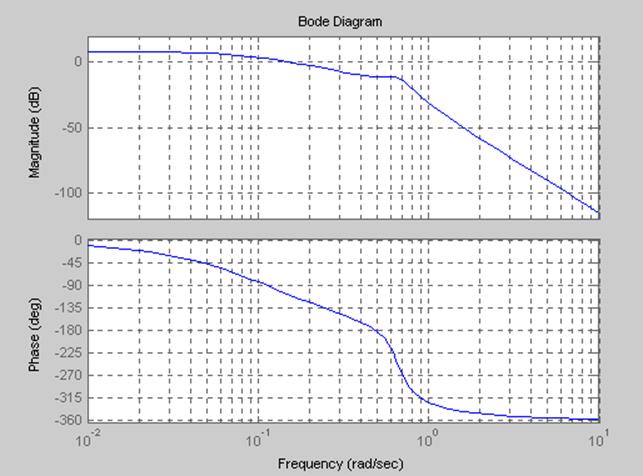
bode(h8),grid                          %диаграммы Боде

h10=feedback(h1,h9)             %передаточная функция замкнутой системы

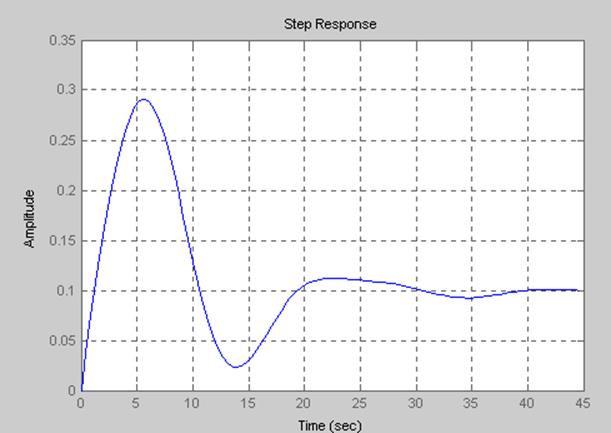
step(h10)                                %переходной процесс в замкнутой системе

Приложение А  График корневого годографа

Приложение Б   Годограф Найквиста

Приложение В   Диаграммы  Боде

Приложение Г   График переходного процесса

Список использованных источников

1.  Андриевский Б.Р. Избранные главы теории автоматического управления с примерами на языке MatLAB. / Б.Р. Андриевский, А.Л.Фрадков. – С.-П.: Наука, 1999.

2.  Ерофеев А.А. Теория автоматизированного управления. – С.-П.: Политехника, 2001.

3.  Ануфриев И.Н. MatLAB 5.3/6x. – СпБ: BHV, 2002. – 736 с.