Моделирование объектов систем компьютерного управления: сбор и фиксация результатов моделирования. Вариант № 3, страница 2

 - характеристическое уравнение

- корни характеристического уравнения

Находим точку бифуркации:

Будем рассматривать случаи:

а) , б) , в)  

Общее решение однородного уравнения:

  - в случае действительных корней

- в случае одного действительного корня

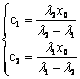
- в случае комплексно-сопряженных корней

5. Эксперимент:

Теоретические графики были получены с помощью Matlab.

Система уравнений для решения в Matlab:

5.1.

5.1.1. , - пара комплексно-сопряженных корней

Решение:

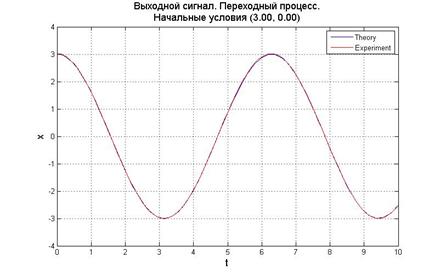
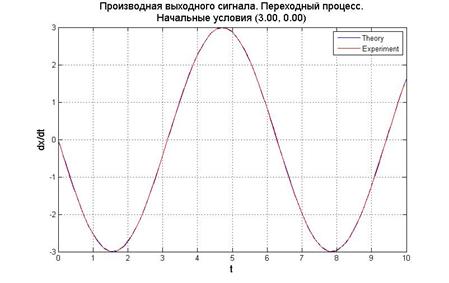
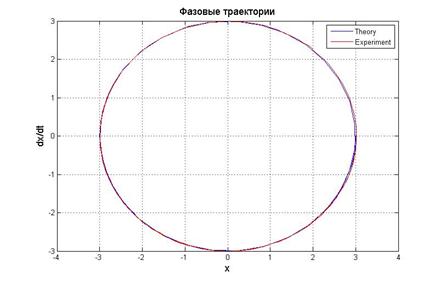
Рис.5.1.1. График выходного сигнала, его производной и фазовый портрет

5.1.2. , - пара комплексно-сопряженных корней

Решение:

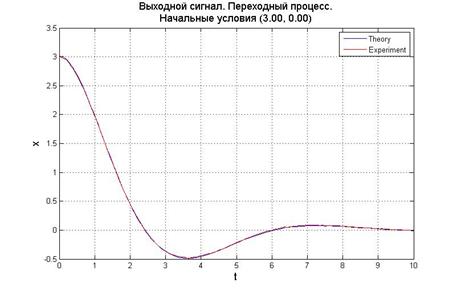
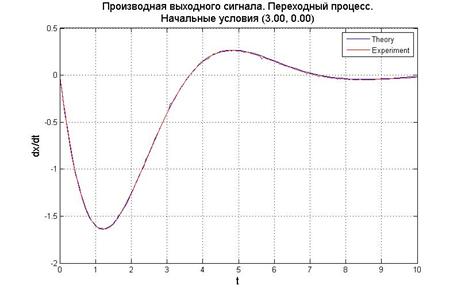
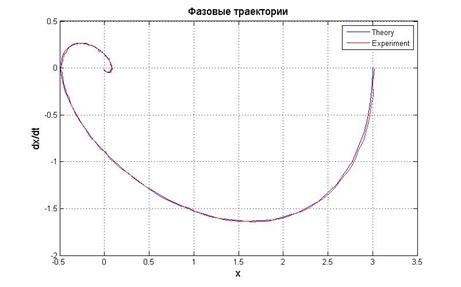
Рис.5.1.2. График выходного сигнала, его производной и фазовый портрет

5.1.3. , - один действительный корень

Решение:

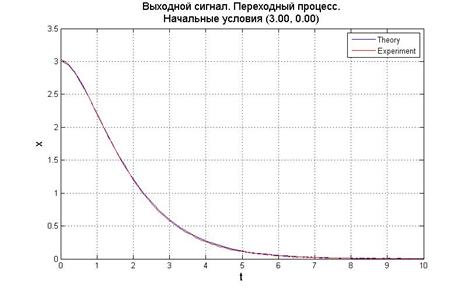
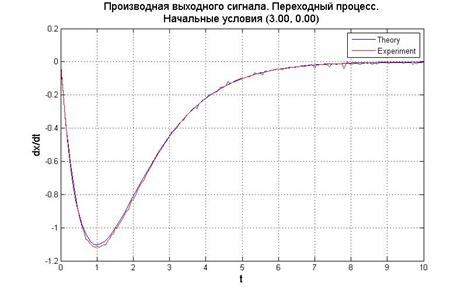
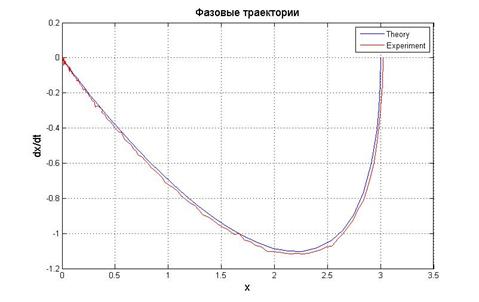
Рис.5.1.3. График выходного сигнала, его производной и фазовый портрет

5.1.4. ,  - два действительных корня

Решение:

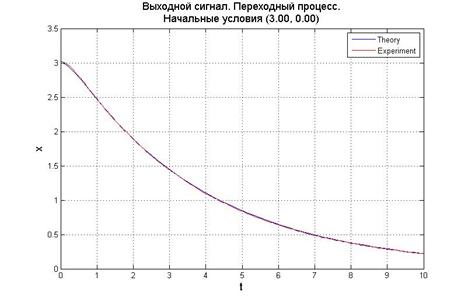
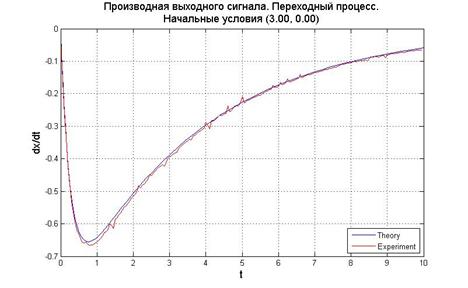
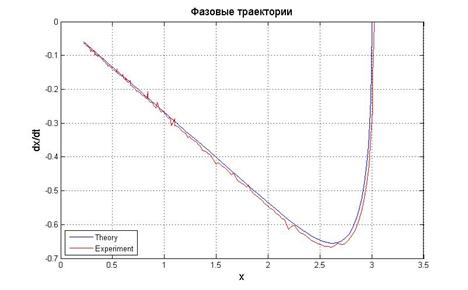
Рис.5.1.3. График выходного сигнала, его производной и фазовый портрет

5.2.

5.2.1. ,