Коагулянты – растворы электролитов (наиболее часто сульфат алюминия или хлористое железо). Их механизм основан на нейтрализации поверхностного заряда на поверхности тонкодисперсных частиц и последующей коагуляцией (слипанием) частиц также с образованием агломератов, имеющих обычно хлопьевидную или более прочную структуру. Иногда смесь предварительно подвергают термической обработке. В результате всех указанных видов обработки получаю осадок с меньшим сопротивлением. Таким образом можно перевести неразделяемую суспензию в разделяемую (например, шлам коммунальных сточных вод может коагулироваться хлористым железом, а затем может обрабатываться флокулянтами).
Скорость фильтрования во многом зависит от пористости фильтрующей перегородки, ее способности к закупориванию. Размер пор фильтра должен быть настолько большим, насколько это возможно для уменьшения быстрого закупоривания, и настолько мал, насколько это необходимо для предотвращения прохождения через фильтр тонкодисперсных твердых частиц. Толстые жесткие фильтры склонны к закупориванию в большей степени, чем тонкие гибкие.
Полученные кинетические закономерности процесса фильтрования справедливы для несжимающихся осадков. При расчете процессов фильтрования с образованием сжимаемого осадка используют уравнения, описывающие кинетику процессов фильтрования с образованием несжимаемых осадков, и средние значения удельного сопротивления осадка и сопротивления фильтрующей перегородки.
11.3. Уравнения фильтрования для различных режимов процесса
Постоянная разность давлений. При Δp = const интегрирование уравнения (11.5) в пределах от 0 до V и от 0 до τ приводит к выражению:
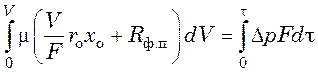 ,
,
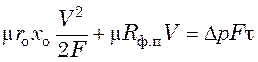 .
.
Разделив обе
части на 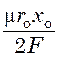 получим:
получим:
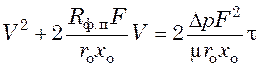 . (11.8)
. (11.8)
Согласно полученному уравнению при постоянном перепаде давления продолжительность фильтрования пропорциональна квадрату объема получаемого фильтрата.
При Δp = const для фильтра данной конструкции и данной фильтровальной перегородки все входящие в уравнение (11.8) величины, кроме V и τ, постоянны, поэтому его можно представить в виде
![]() (11.9)
(11.9)
где 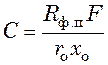 , а
, а 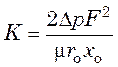 – константы фильтрования, характеризующие
свойства фильтровальной перегородки и осадка, соответственно.
– константы фильтрования, характеризующие
свойства фильтровальной перегородки и осадка, соответственно.
Постоянная
скорость процесса. При (dV/dτ = const) уравнение
фильтрования (11.5) решается следующим путем. Отношение dV/dτ
можно заменить равным ему V/τ и решить относительно ![]() :
:
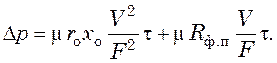 (11.10)
(11.10)
Умножив и разделив
первое слагаемое правой части этого уравнения на ![]() ,
получим
,
получим
![]() (11.11)
(11.11)
Уравнение (11.11) показывает, что при w=dV/dτ = const разность давлений возрастает с течением времени.
Постоянная
скорость и постоянная разность давлений. Такой вид фильтрования реализуется,
если чистая жидкость фильтруется через слой осадка, иными словами, производится
промывка осадка методом вытеснения при постоянной разности давлений. Если ![]() и
и ![]() ,
уравнение (11.5) переписывается в виде:
,
уравнение (11.5) переписывается в виде:
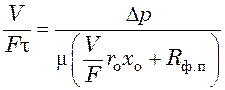 .
.
Заменив в
последнем выражении 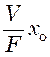 эквивалентной величиной толщины
осадка h0, получим:
эквивалентной величиной толщины
осадка h0, получим:
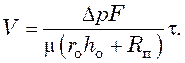 (11.12)
(11.12)
На большинство
фильтров, работающих под давлением, суспензия на фильтрование подается
центробежным насосом. Центробежные насосы не поддерживают постоянную скорость
или постоянное давление, а имеют, как известно, определенную характеристику
вида ![]() или
или ![]() , где
, где ![]() – напор, а
– напор, а ![]() давление,
создаваемое насосом. Фильтрование в этом случае протекает при возрастающем
давлении и уменьшающейся скорости (
давление,
создаваемое насосом. Фильтрование в этом случае протекает при возрастающем
давлении и уменьшающейся скорости (![]() ,
,![]() ). В этом случае для интегрирования
уравнения (11.5) в него можно подставить
). В этом случае для интегрирования
уравнения (11.5) в него можно подставить ![]() ,
выраженное аналитической зависимостью, а решение будет проще всего, получить
численными методами с использованием ЭВМ.
,
выраженное аналитической зависимостью, а решение будет проще всего, получить
численными методами с использованием ЭВМ.
11.4. Определение констант в уравнениях фильтрования
Полученное для условий постоянного перепада давлений уравнение (11.9) позволяет переносить результаты лабораторных исследований процесса фильтрования на промышленные масштабы процесса.
В самом деле, входящие в константы фильтрования величины зависят
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.