График зависимости M = f(N)
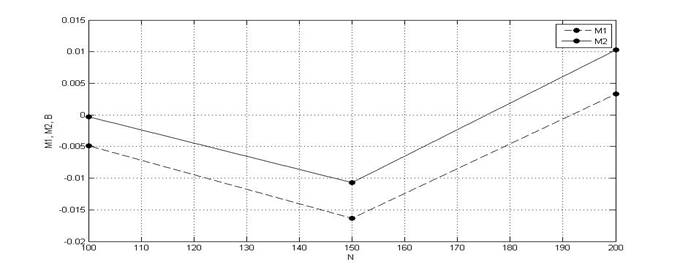
Рис.16.
График зависимости SK = f(N)
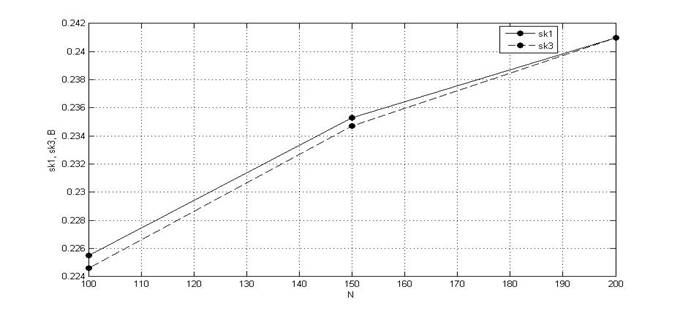
Рис.17.
4.4.Анализ измерения полезного сигнала в условиях помех типа белого шума.
Результаты согласно файлам из программы Opros.
C канала 1 снимается полезный сигнал; с канала 2 – белый шум.
Ниже приведены графики для U=0; U = const = 2; U = sin.
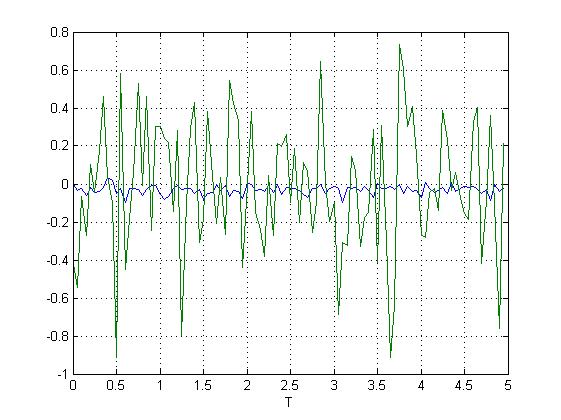
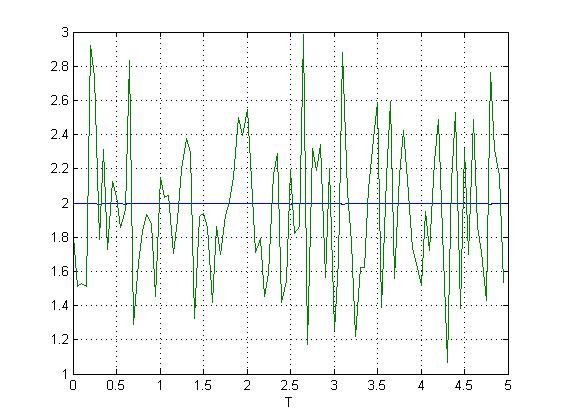
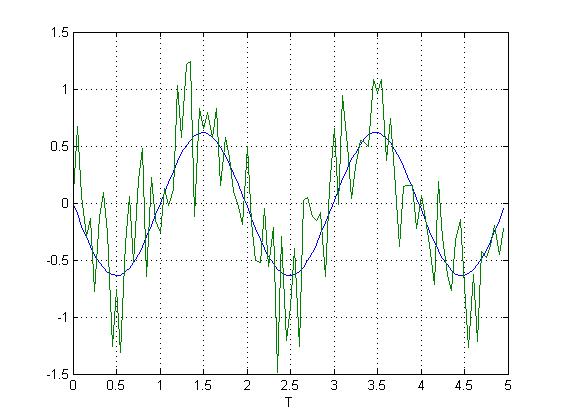
Рис.30. Измерение сигнала с объекта при наложении помех.
5. Выводы
Изменяя значения х на входе первого канала (АЦП), можно получить оценку точности работы подсистем ввода-вывода во всем диапазоне возможного изменения сигналов на входе АЦП и ЦАП.
Усилитель У1 (см. рис.1.) вносит в результат дополнительную помеху: имеется отклонение в 2 стороны на канале 1. Смещение нуля усилителя вносит погрешность на входе АЦП, таким образом, на выходе получаем сигнал с погрешностью, который вновь подается на вход подсистемы. Тогда суммарную погрешность подсистемы вывода можно рассматривать: величина измеряемого сигнала – 2 погрешности ввода.
В случае детерминированного постоянного сигнала на входе математичекое ожидание сигнала на входе возрастает пропорционально амплитуде Uвх.
Изменение дискретности и объема выборки при постоянной амплитуде входного сигнала не оказывает существенного влияния на точностные характеристики (g1, g2), математическое ожидание постоянно.
Для гармонического сигнала математическое ожидание на бесконечности равно 0. Чем больше период дискретизации, тем больше разница между мат. ожиданиями.
Для случайного сигнала оценка точностных характеристик производится путем усреднения нескольких измерений для одного и того же значения параметра (a, T, N).
В случае, когда на полезный сигнал наложена помеха типа “белого шума” общий вид характер сигнала сохраняется. Для ослабления или устранения шумов в таких сигналах нужно применять аналоговые или цифровые фильтры.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.