теплообмена а. С этой целью выразим плотность теплового потока у поверхности стенки через уравнения Ньютона — Рихмана для теплоотдачи (10.1) и Фурье для теплопроводности (8.3):
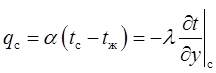(10.7)
где у —
координата, нормальная к поверхности стенки и отсчитываемая от ее поверхности, м; л— теплопроводность
жидкости, Вт/(м∙К); 
— модуль градиента температуры в пограничном слое у поверхности
стенки, К/м.
Уравнение (10.7) называют дифференциальным уравнением теплоотдачи, решив которое
относительно коэффициента теплообмена а, получим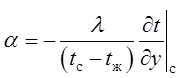 
(10.8)
Расчет коэффициента теплообмена а по уравнению (10.8) с предварительным интегрированием системы дифференциальных уравнений (10.3), (10.5), (10.6) при соответствующих условиях однозначности представляет собой трудновыполнимую задачу, редко реализуемую на практике. Аналитическое решение удается получить лишь для отдельных частных случаев после соответствующих упрощений, а численные решения с применением ЭВМ требуют большего объема работы.
10.5. ПРИМЕНЕНИЕ ТЕОРИИ ПОДОБИЯ ДЛЯ ОПИСАНИЯ ТЕПЛООТДАЧИ
В связи с указанными трудностями аналитического или численного расчета коэффициента теплообмена на основе интегрирования дифференциальных уравнений конвективного теплообмена на практике для описания явлений теплоотдачи широкое распространение получила теория подобия, представляющая собой учение о подобных явлениях.
В технике понятие геометрического подобия распространяется на подобие физических явлений. Геометрическое подобие выражается в пропорциональности сходных линейных размеров тел:
(10.9)
где l1', , l2', l3' — характерные размеры первого тела; l1", l2", l3" — характерные размеры второго тела; Cl — константа геометрического подобия.
Константа геометрического подобия Cl представляет собой масштаб подобных тел. Подобными могут быть далее поля физических 1величин в геометрически подобных системах, различающихся лишь масштабом, если сходственных точках этих
121
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
