Дифференциальные уравнения конвективного массо- и теплообмена

одной или другой фазе, например при C₁>C_p1:

                                                         (14,8)

или

                                                          (14.9)

где m — количество распределяемого вещества, передаваемого из фазы 1 в фазу 2 через поверхность раздела фаз А в единицу времени, кг/с; C_P1 и С_Р2 — равновесные концентрации.

Разности концентраций (C₁—C_P1) и (C_p2—C₂) в уравнениях (14.8) и (14.9) называют движущими силами массопередачи (соответственно по первой и второй фазам), которые берут по модулю (от большей концентрации вычитают меньшую). Коэффициенты пропорциональности K₁ и К₂в этих уравнениях — коэффициенты, массопередачи: они связаны друг с другом соотношением

               (14.10)

Размерность коэффициента массопередачи зависит от способа выражения концентраций: если концентрации выражены в кг/м³, am — в кг/с, то коэффициент массопередачи имеет размерность (м/с). С физической точки зрения коэффициент массопередачи выражает массу распределяемого компонента, прошедшего через единичную поверхность раздела фаз в единицу времени при движущей силе массопередачи, равной единице:

14.5.  ДИФФЕРЕНЦИАЛЬНЫЕ  УРАВНЕНИЯ   КОНВЕКТИВНОГО МАССО-  И ТЕПЛООБМЕНА. ТРОЙНАЯ  АНАЛОГИЯ

Дифференциальное уравнение конвективного массообмена*, описывающее массоперенос в движущейся среде, выводится аналогично дифференциальному уравнению энергии. В отсутствие источников массы уравнение конвективного массообмена при D = const имеет вид

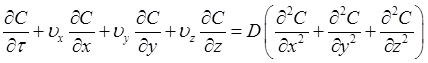           (14.11)

или                                                          (14.12)

где 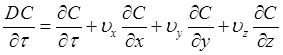         – субстанциальнаяпроизводная;

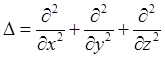– оператор Лапласа;,,– компоненты скорости потока, м/с.

160