Изменение концентрации распределяемого вещества в произвольной неподвижной точке

Первое слагаемое левой части уравнения (14.11) характеризует изменение концентрации распределяемого вещества в произвольной неподвижной точке с координатами х, у, z во времени т; слагаемые с компонентами скорости — изменение концентрации в указанной точке за счет движения потока; слагаемые правой части уравнения — изменение концентрации, вызванное молекулярной диффузией. Уравнение (14.11) записано в общей форме; в частных случаях (одномерное движение, отсутствие молекулярной диффузии и т. д.) оно принимает более простой вид.

При х_x = х_y = х_z = 0 уравнение (14.11) переходит в дифференциальное уравнение молекулярной диффузии (14.3).

Интегрирование уравнения (14.11) при соответствующих условиях однозначности дает значение концентрации как функции координат и времени: С=({х, у, z, ф). Однако это решение может быть получено в аналитическом виде только для наиболее простыхслучаев. В общем случае неоднородного поля скоростей (например, в случае движения потока вблизи поверхности раздела фаз) уравнение (14.11) нужно интегрировать совместно с уравнениями движения Навье — Стокса, описывающими скоростное поле, и уравнением неразрывности, что представляет сложную задачу. Поэтому основным путем исследования конвективного массообмена (как и конвективного теплообмена) является экспериментальный путь с привлечением теории подобия. Цель такого исследования состоит обычно в установлении опытных критериальных зависимостей для расчета коэффициента массообмена.

При маccоотдаче плотность потока массы у поверхности раздела фаз можно выразить через уравнение массообмена (14.5) и через уравнение молекулярной диффузии (14.1):

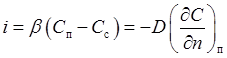                         (14.13)

Преобразуя уравнение (14.13) методами теории подобия, получим массообменное число Нуссельта:

                                                     (14.14)

где l — характерный размер, м.

Анализируя уравнение конвективного массообмена (14.11), получим критерии (числа) Рейнольдса и Прандтля для массообмена:

 и                             (14.15)

где — кинематическая вязкость, м²/с

Число Nu_m выражает соотношение сопротивлений диффузии пограничного слоя R_D =l/D и массоотдачи R_в = 1/в:

161