























































фиксированное положение, не совпадающее с положением равновесия) от
параметров m, l, φ0 и g (параметр v
следует исключить из
рассмотрения, поскольку его удалось выразить через указанные выше параметры).
Размерности [•] четырех указанных параметров и периода Т колебаний можно
выразить через k = 3 независимые стандартные единицы измерения: [Т] =
с, [m] = = кг, [l] = м, [φ0] = 0 и [g] = м/с2.
Поэтому в силу П-теоремы из n = 5
параметров можно составить ![]() безразмерные комбинации,
причем угол φ0, будучи безразмерным, является одной из них.
Во вторую безразмерную комбинацию не удается включить массу m материальной точки, поскольку единица измерения массы (кг) входит
лишь в размерность массы. Следовательно, величина m не является аргументом искомой зависимости, что можно установить
и при построении теоретической ММ рассматриваемого маятника. После исключения
параметра m имеем n = 4 и k = 2, т.е. снова
безразмерные комбинации,
причем угол φ0, будучи безразмерным, является одной из них.
Во вторую безразмерную комбинацию не удается включить массу m материальной точки, поскольку единица измерения массы (кг) входит
лишь в размерность массы. Следовательно, величина m не является аргументом искомой зависимости, что можно установить
и при построении теоретической ММ рассматриваемого маятника. После исключения
параметра m имеем n = 4 и k = 2, т.е. снова ![]() , так что наряду с
безразмерным параметром φ0 остальные параметры образуют лишь
одну независимую безразмерную комбинацию, которую можно представить в виде
, так что наряду с
безразмерным параметром φ0 остальные параметры образуют лишь
одну независимую безразмерную комбинацию, которую можно представить в виде ![]()
Таким образом, согласно П-теореме, искомую зависимость можно искать в виде
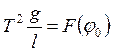 , или
, или 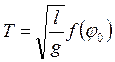 , (2.2)
, (2.2)
где ![]() –
некоторая функция угла φ0.
Установить вид этой функции в рамках теории размерностей нельзя. Для
этого необходимо либо провести эксперимент и обработать его результаты в
соответствии с первым равенством (2.2), выявив функциональную зависимость
безразмерной комбинации
–
некоторая функция угла φ0.
Установить вид этой функции в рамках теории размерностей нельзя. Для
этого необходимо либо провести эксперимент и обработать его результаты в
соответствии с первым равенством (2.2), выявив функциональную зависимость
безразмерной комбинации ![]() от φ0,
либо воспользоваться теоретической ММ, которая представляет функцию f в виде полного эллиптического
интеграла первого рода. Но даже при неизвестных функциях f (или F) при помощи (2.2)
можно получить полезные результаты. Например, если известно значение периода Т колебаний
для некоторого маятника длиной l при
фиксированных значениях g
и φ0, то
для маятника длиной l1 период колебаний будет равен
от φ0,
либо воспользоваться теоретической ММ, которая представляет функцию f в виде полного эллиптического
интеграла первого рода. Но даже при неизвестных функциях f (или F) при помощи (2.2)
можно получить полезные результаты. Например, если известно значение периода Т колебаний
для некоторого маятника длиной l при
фиксированных значениях g
и φ0, то
для маятника длиной l1 период колебаний будет равен ![]() .
.
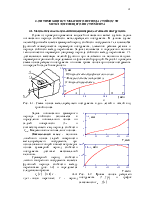
Из соображений симметрии (см.
рис. 2.3) значение периода колебаний не должно зависеть от знака угла φ0
первоначального отклонения маятника. Поэтому функция f(φ0) должна быть четной. Предполагая ее дважды
непрерывно дифференцируемой в некоторой окрестности точки φ0
= 0 и используя формулу Тейлора с остаточным членом в форме Лагранжа, можно
записать 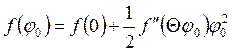 , где
, где ![]() . Если
при φ0→0 ограничиться лишь первым слагаемым в правой части
этого равенства, то из (2.2) получим
. Если
при φ0→0 ограничиться лишь первым слагаемым в правой части
этого равенства, то из (2.2) получим ![]() .
.
Таким образом, теория размерностей позволяет установить зависимость для периода бесконечно малых колебаний математического маятника с точностью до постоянного множителя f(0). Соответствующая этому случаю хорошо известная теоретическая ММ приводит к значению f(0)=2π.
Пример 2.2. К полуэмпирической следует отнести ММ, включающую известную формулу
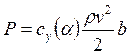 (2.3)
(2.3)
 для подъемной силы крыла в дозвуковом воздушном потоке, приходящейся
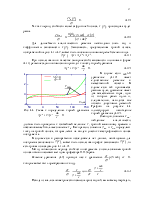
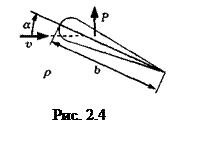
на единицу длины размаха крыла (здесь ρ и v – плотность и скорость набегающего потока, b – так называемая хорда профиля крыла (рис. 2.4), су(α)
– безразмерный коэффициент, зависящий от формы профиля крыла и характеризуемого
углом атаки α направления набегающего потока). Угол атаки и параметры,
определяющие форму профиля крыла, безразмерны. Поэтому можно рассматривать
влияние n = 4 размерных параметров Р, ρ,
v и b,
размерности которых можно выразить через k = 3 независимые
стандартные единицы измерения: [Р] = Н/м = кг/с2, [ρ] = кг/м3,
[v] = м/с, [b] = м, где Н =
для подъемной силы крыла в дозвуковом воздушном потоке, приходящейся
на единицу длины размаха крыла (здесь ρ и v – плотность и скорость набегающего потока, b – так называемая хорда профиля крыла (рис. 2.4), су(α)
– безразмерный коэффициент, зависящий от формы профиля крыла и характеризуемого
углом атаки α направления набегающего потока). Угол атаки и параметры,
определяющие форму профиля крыла, безразмерны. Поэтому можно рассматривать
влияние n = 4 размерных параметров Р, ρ,
v и b,
размерности которых можно выразить через k = 3 независимые
стандартные единицы измерения: [Р] = Н/м = кг/с2, [ρ] = кг/м3,
[v] = м/с, [b] = м, где Н = 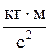 (ньютон)
– производная единица измерения силы. Согласно П-теореме, из этих размерных
параметров можно составить лишь одну (
(ньютон)
– производная единица измерения силы. Согласно П-теореме, из этих размерных
параметров можно составить лишь одну (![]() ) независимую
безразмерную комбинацию, которую запишем в виде
) независимую
безразмерную комбинацию, которую запишем в виде ![]() . Тогда
для конкретной формы профиля крыла получим
. Тогда
для конкретной формы профиля крыла получим
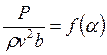
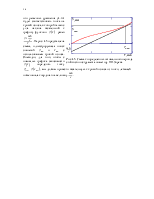
где функция f(α) может быть найдена экспериментально путем продувки под различными углами атаки геометрически подобной модели крыла
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.