 Ответ: по методу Лэнгли (Samuel P.
Langley). Спектральная плотность потока
прямого солнечного излучения
Ответ: по методу Лэнгли (Samuel P.
Langley). Спектральная плотность потока
прямого солнечного излучения ![]() , достигающего
поверхности Земли, согласно закону Бугера, равна
, достигающего
поверхности Земли, согласно закону Бугера, равна
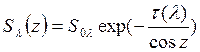 ,
,
где z - зенитный угол
Солнца, ![]() - оптическая толщина атмосферы в
вертикальном направлении для заданной длины волны,
- оптическая толщина атмосферы в
вертикальном направлении для заданной длины волны, ![]() -
искомая спектральная плотность солнечного излучения на верхней границе
атмосферы. Приведенное соотношение не учитывает кривизну атмосферы, поэтому
оно справедливо для не слишком больших зенитных углов Солнца. Сделаем замену[6]:
-
искомая спектральная плотность солнечного излучения на верхней границе
атмосферы. Приведенное соотношение не учитывает кривизну атмосферы, поэтому
оно справедливо для не слишком больших зенитных углов Солнца. Сделаем замену[6]:
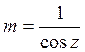 . Тогда
. Тогда
![]() .
.
Отсюда следует, что искомая величина ![]() . Конечно, мы не можем дождаться ситуации,
когда относительная воздушная масса
. Конечно, мы не можем дождаться ситуации,
когда относительная воздушная масса ![]() обратится в ноль (самое
меньшее, что можно получить, это
обратится в ноль (самое
меньшее, что можно получить, это ![]() , и то только в районе
экватора. Можно, однако, экстраполировать данные наблюдений, полученные для
ряда значений
, и то только в районе
экватора. Можно, однако, экстраполировать данные наблюдений, полученные для
ряда значений ![]() , на нулевую воздушную массу.
Это довольно легко сделать, поскольку все результаты наблюдений должны лежать
вблизи прямой линии, согласно приведенной выше формуле (с учетом ошибок
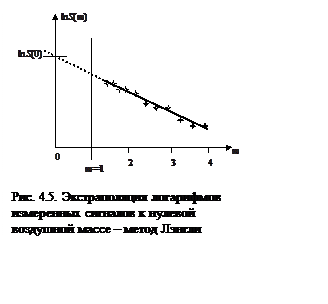
измерений). Нужно только провести достаточно много измерений сигналов. Схема,
иллюстрирующая процедуру, представлена на рис. 4.5. Обратите внимание, что
тангенс угла наклона прямой непосредственно определяет вертикальную оптическую
толщину атмосферы -
, на нулевую воздушную массу.
Это довольно легко сделать, поскольку все результаты наблюдений должны лежать
вблизи прямой линии, согласно приведенной выше формуле (с учетом ошибок
измерений). Нужно только провести достаточно много измерений сигналов. Схема,
иллюстрирующая процедуру, представлена на рис. 4.5. Обратите внимание, что
тангенс угла наклона прямой непосредственно определяет вертикальную оптическую
толщину атмосферы - ![]() .
.
Именно
так раньше и проводились эксперименты. Точность, однако, была не очень высокой.
Основной проблемой при применении метода является требование стабильности атмосферы
(постоянства ![]() )
в течение всего срока наблюдений. На земном шаре не так уж много мест, где это
требование выполняется достаточно часто.
)
в течение всего срока наблюдений. На земном шаре не так уж много мест, где это
требование выполняется достаточно часто.
Прецизионные измерения солнечных спектров и солнечной постоянной были проведены в последние годы с использованием аппаратуры, выводимой за пределы атмосферы.
[1] Происхождение названия «сечение» легко понять, если рассмотреть процесс бомбардировки тонкого слоя вещества частицами пренебрежимо малого размера. Пусть слой настолько тонок, что на площадь в 1см2 приходится по одному атому вещества и пусть этот атом представляется твердым шариком радиуса . Тогда доля частиц, падающих на 1см2 слоя и сталкивающихся с атомом, очевидно, равна - площади сечения шарика. Другими словами, сечение поглощения определяет вероятность поглощения фотона одним атомом или молекулой в единицу времени при единичной плотности потока излучения.
Обычно сечение поглощения сильно зависит от длины волны падающего излучения. Поэтому пишут , относя величину сечения к единичному интервалу длин волн согласно формуле , где - спектральная (отнесенная к единичному интервалу длин волн) плотность потока падающего излучения.
[2] Число Лошмидта связано с числом Авогадро NA=6.022·1023 моль-1 - числом молекул в одном моле газа. При нормальных условиях моль газа занимает объем V=22.4 ·10 3 см3. Следовательно, .
[3] Согласно приведенному определению, коэффициент поглощения численно равен оптической толщине единичной ширины слоя газа, приведенного к нормальным условиям.
[4] Здесь уместна аналогия с просеиванием песка сквозь решето. Представьте, что на высоте термосферы установлена сетка с крупными ячейками, задерживающая самые «крупные» (то есть, самые энергичные) фотоны. За счет «пойманных» фотонов и происходит нагрев этой области атмосферы. В мезосфере установлена сетка с почти такими же ячейками. Очевидно, эта сетка не сможет «отловить» сколько-нибудь значительное число фотонов, потому что мелкие «проскакивают» сквозь нее, а «крупных» уже нет. На высоте стратосферы находится сетка с более мелкими ячейками, и там опять начинается «отлов» фотонов. Они уже не так энергичны, как те, что задержаны в термосфере, однако их достаточно, чтобы создать слой с повышенной температурой.
[5] На самом деле следует учитывать еще ряд факторов – кривизну атмосферы, рассеяние излучения, вертикальный и горизонтальный перенос и «уничтожение» продуктов фотолиза в других реакциях.
[6] Величину m называют относительной воздушной массой. Она показывает во сколько раз наклонный путь через атмосферу длиннее, чем путь в вертикальном направлении (z=0). При больших значениях зенитных углов Солнца выражение для относительной воздушной массы следует скорректировать, чтобы учесть кривизну атмосферы. Для этого, вообще говоря, нужно знать хотя бы приблизительно вертикальное распределение основных ослабителей солнечного излучения выбранной длины волны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.