Атмосферное электричество. Методы изучения ионизационного состояния атмосферы. Электрическое поле в атмосфере, страница 4

                   Таблица 9.1. Оценка проводимости воздуха в зависимости от высоты [1]

Эта зависимость описывается следующим соотношением

                                 .

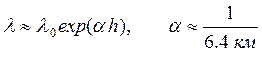Приведенные оценки были получены много лет назад и весьма приближенны. Особенно это касается больших высот. Более точные расчеты дают значение электрической проводимости воздуха на высоте около 100 км в пределах 10⁵-10⁶ с^-1. Это обусловлено, в первую очередь, влиянием солнечных и космических ионизирующих излучений.

9.3. Электрическое поле в атмосфере

Уже очень давно установлено, что Земля обладает отрицательным зарядом и, как всякое заряженное тело,  соответствующим электрическим полем. Электрическое поле в атмосфере характеризуется значением потенциала V в каждой точке. Тогда напряженность поля  (является градиентом потенциала с обратным знаком).

Соединяя  точки с одинаковым значением потенциала, получаем изопотенциальные (эквипотенциальные) поверхности. Они не могут пересекаться и касаться друг друга, поскольку в противном случае в точке соприкосновения наблюдались бы разные потенциалы. Они сближаются там, где напряженность поля выше, и расходятся, где она уменьшается. В частности, напряженность поля резко возрастает в области острых углов на проводящей заряженной поверхности, остро заточенных проводников и т.п. Поверхность самого проводника в случае статических полей является эквипотенциальной поверхностью.

Принимая поверхность Земли за проводник (что весьма неплохо соответствует действительности), имеем

             E₀= - dV/dh=4πσ  (в единицах CГСЭ),    E₀= - dV/dh=σ/ε₀ (в единицах СИ),

где σ­ поверхностная плотность заряда. При наличии в атмосфере объемных зарядов (такое бывает) для нахождения напряженности поля нужно решать уравнение Пуассона для электрического потенциала

               ΔV=-4πρ(x,y,z), (в единицах CГСЭ), ΔV=-ρ(x,y,z) /ε₀, (в единицах CИ)

где ρ - объемная плотность зарядов, 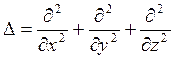 - оператор Лапласа. Кроме того, если быть совсем уж последовательным, следует учитывать электрическую проводимость атмосферы.

Наблюдения у земной поверхности дают величину напряженности поля около 130 B/м,   что соответствует поверхностной плотности заряда σ=7·10⁵e/см². Здесь в качестве единицы измерений использован элементарный заряд электрона e=1.6·10^-19 Кл. Умножая на площадь всей Земли, находим заряд Q= - 5,7·10⁵ Кл, а потенциал V=Q/c, где емкость c=R в единицах СГСЭ (в системе единиц СИ с=4πε₀R, ε₀≈9·10^-12 Ф/м). Поэтому для потенциала Земли имеем V=Q/(4πε₀R ) ~ -10⁹ B. 

Наиболее распространенными методами изучения электрического поля Земли являются метод коллектора и метод пластины. Коллекторами называются различного рода приспособления, принимающие потенциал точки атмосферы, в которой расположены.  Простейший коллектор - изолированный проводник с острием (лишние заряды стекают с острия). На практике используют более эффективные коллекторы в виде пламени свечи, разбрызгиваемой воды, покрытых радиоактивным веществом металлических пластинок и т.д. Их действие сводится к уносу несвязанного заряда с отделяющимися частичками или к повышению проводимости воздуха в окрестности проводника за счет ионизации. Соединив коллектор через электрометр с заземленным электродом, можно измерить потенциал в некоторой точке атмосферы по отношению к Земле.