7.3. Простейшие типы точек.
Исследуем расположение траекторий в
окрестности точки покоя ![]() системы 2 линейных однородных уравнений с
постоянным коэффициентом.
системы 2 линейных однородных уравнений с
постоянным коэффициентом.
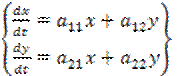 , (7.7)
, (7.7)
где 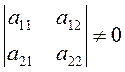 .
.
Имеем решения в виде ![]() . Для определения k пишем
характеристическое уравнение:
. Для определения k пишем
характеристическое уравнение:
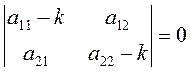
или
![]() .
.
Числа
![]() с точностью до постоянного множества
определяется из одного уравнения:
с точностью до постоянного множества
определяется из одного уравнения:
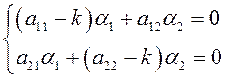 , (7.8)
, (7.8)
а) Корни характеристического уравнения k1 и k2 действительны и различны. Общее решение имеет вид:
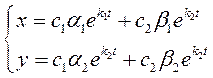 (7.9),
(7.9),
где ![]() -
постоянные, определяемые из уравнения (7.8), соответственно при
-
постоянные, определяемые из уравнения (7.8), соответственно при ![]() и при
и при ![]() , а
, а ![]() -
произвольные постоянные.
-
произвольные постоянные.
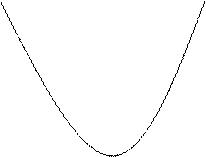
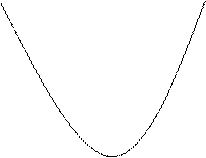
При этом возможны следующие случаи:
|
|
 д
д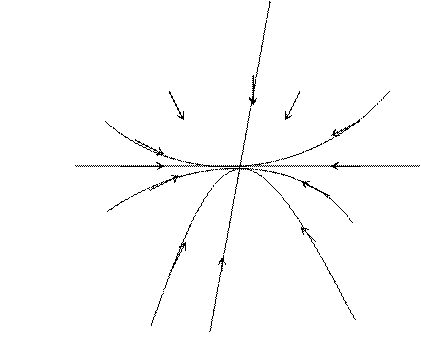
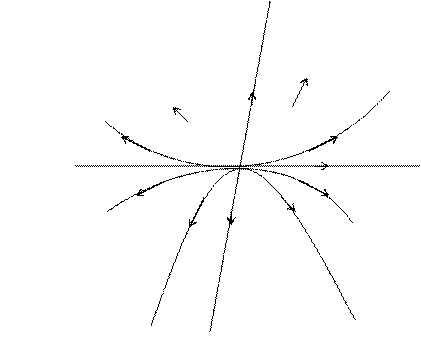
данного типа, называемой устойчивым узлом. Стрелками показано направление движения траектории при возрастании t.
2) k1![]() 0 и k2
0 и k2![]() 0. Этот случай
переходит в предыдущее при замене t на (-t), поэтому
траектории будут те же, только движение в обратном направлении (рис. 7.2).
0. Этот случай
переходит в предыдущее при замене t на (-t), поэтому
траектории будут те же, только движение в обратном направлении (рис. 7.2).
Точки близкие к началу координат будут отдаляться , значит точка покоя – неустойчивый узел.
 3) Если k1
3) Если k1![]() 0 и k2
0 и k2![]() 0, то точка покоя
тоже неустойчива, т.к. движущаяся по
0, то точка покоя
тоже неустойчива, т.к. движущаяся по 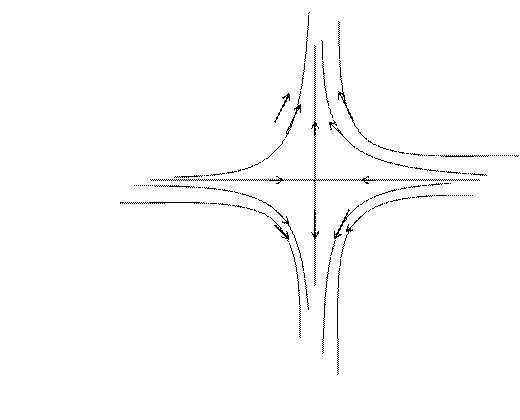 траектории
траектории ![]() (7.10)
(7.10)
|
![]() - движение по этой прямой к началу
координат. Движение (7.10) по прямой
- движение по этой прямой к началу
координат. Движение (7.10) по прямой
от начала координат.
Если же С1
и С2 ≠ 0, то при ![]() траектории покидают окрестности начала
координат , такая точка покоя называется седлом, так как расположение
траектории в её окрестности напоминает линии уровня в окрестности седлообразной
точки некоторой поверхности.
траектории покидают окрестности начала
координат , такая точка покоя называется седлом, так как расположение
траектории в её окрестности напоминает линии уровня в окрестности седлообразной
точки некоторой поверхности.
б) Корни характеристического уравнения комплексны
![]()
Общее решение системы (7.7) можно записать в виде
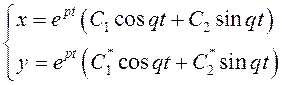
Где С1 и С2 - произвольные постоянная, С1* и С2* - некоторые линейные комбинации этих постоянных.
Возможны следующие случаи:
·
![]()
Если бы было ![]() , то траекториями были бы замкнутые кривые,
окружающие точку покоя
, то траекториями были бы замкнутые кривые,
окружающие точку покоя ![]() (Рис. 7.4.).
(Рис. 7.4.).

Наличие
направляющегося к 0 множителя ![]() превращает
замкнутые кривые в спирали, асимптотически приближающиеся к началу координат
(рис. 7.5.)
превращает
замкнутые кривые в спирали, асимптотически приближающиеся к началу координат
(рис. 7.5.) 
Точка покоя – асимптотически устойчива, она называется фокусом.
·
![]() .
.
Этот случай переходит в предыдущий при замене t на (-t) и движение будет в обратную сторону (от начала координат). Точка покоя неустойчива, т.к. отдаляется от начала координат.
· 
· ![]() .
.
Траекториями являются кривые, содержащие точки покоя, называют в этом случае центром (Рис 8.4). Эта точка устойчива, но асимптотической устойчивости нет.
в) Корни кратны ![]()
Общее решение имеет вид 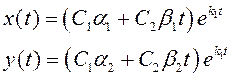 ,
,
 причем не исключен случай
причем не исключен случай ![]() ,
но тогда
,
но тогда ![]() будут произвольными постоянными.
будут произвольными постоянными.
Точка покоя называется устойчивым узлом (Рис. 8.7).
Точка покоя асимптотически устойчива.
Если![]() , то получаем устойчивый узел, он
называется дикритическим узлом (Рис. 8.8)
, то получаем устойчивый узел, он
называется дикритическим узлом (Рис. 8.8)
· ![]()
Замена переменных t на (-t) сводит к
предыдущему случаю, только движение по траектории будет направлено в другую
сторону, точка покоя называется неустойчивым узлом. Тем самым исчерпаны
все возможности, т.к. случай ![]() (или
(или ![]() ) исключается условием
) исключается условием 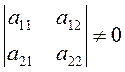 .
.
Пусть ![]() , тогда решение системы (7.7) имеет вид:
, тогда решение системы (7.7) имеет вид:
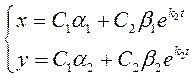
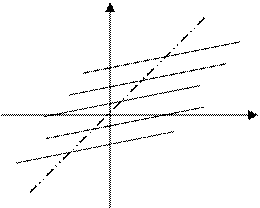
Исключая tполучим семейство параллельных прямых:
![]() .
.
Точка покоя устойчива, если ![]() , но асимптотической устойчивости нет и при
, но асимптотической устойчивости нет и при
![]() движение
происходит, приближаясь к точке покоя:
движение
происходит, приближаясь к точке покоя: ![]() .
.

При ![]() движение происходит в обратном направлении
и точка покоя неустойчива.
движение происходит в обратном направлении
и точка покоя неустойчива.
Если ![]() , то возможно два
случая:
, то возможно два
случая:
1. Общее решение системы (7.1) имеет вид:
![]() .
.
Т.е. все точки являются точками покоя, все решения устойчивы
2. ![]() ,
,
![]() - линейные комбинации производных
постоянных
- линейные комбинации производных
постоянных ![]() . Точка покоя
. Точка покоя ![]() неустойчива.
неустойчива.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.