Закономерности теплового излучения: Учебно-методическое обеспечение практического занятия, страница 2

                                            ,                                            (5.2)

где  – постоянная Стефана–Больцмана;  – термодинамическая температура.

Из выражений (5.1) и (5.2) получим формулу для мощности излучения:

                                           .                                           (5.3)

Подставив значения величин в формулу (5.3), найдем

                  Вт.

Ответ:  Вт.

Пример 6.  Найти с помощью формулы Планка мощность излучения с площади 15,0  абсолютно черного тела, приходящуюся на узкий интервал длин волн, равный 5,00 нм, вблизи максимума спектральной плотности излучения при температуре тела 1000 К.

Энергетическая светимость  абсолютно черного тела связана со спектральной плотностью энергетической светимости :

                                          .                                           (6.2)

Для узкого интервала длин волн можно записать

                                           .                                           (6.3)

По условию задачи для расчета спектральной плотности энергетической светимости  следует использовать формулу Планка

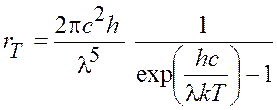                              .                              (6.4)

Поскольку интервал длин волн задан вблизи максимума спектральной плотности излучения, то для нахождения длины волны, входящей в формулу Планка, воспользуемся законом смещения
Вина:

                                               .

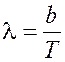Из выражений (6.1) – (6.4) получим формулу для мощности излучения:

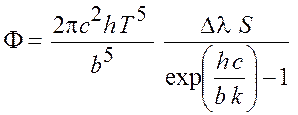                            .                            (6.5)

Подставив значения величин в формулу (6.5), найдем

                

    .

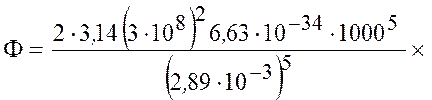
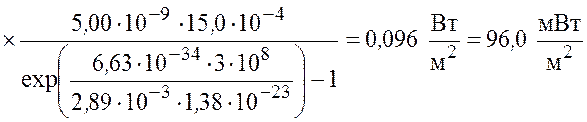Ответ: .

Пример 7.  Замкнутая полость объемом 1,00 л заполнена тепловым излучением (фотонным газом), температура которого 1000 К. Найти энтропию и теплоемкость теплового излучения.

– теплоемкость при постоянном объеме

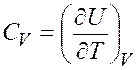                                         ,                                          (7.1)

где U – энергия системы;

– связь теплоемкости и энтропии:

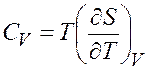                                        .                                         (7.2)

Из формул (7.1) и (7.2) получим зависимость энтропии от температуры при постоянном объеме:

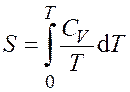                                          .                                          (7.3)

Объемная плотность энергии изотропного излучения, каким в частности является равновесное тепловое излучение,

                                            ,

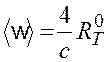где с – скорость света в вакууме;  – энергетическая светимость абсолютно черного тела.

Энергия излучения (фотонного газа), заключенного в объеме V,

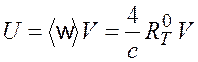                                    .                                     (7.4)

Энергетическая светимость  абсолютно черного тела выражается законом Стефана–Больцмана:

                                            ,                                            (7.5)

где  – постоянная Стефана–Больцмана;  – термодинамическая температура.

Подставив (7.5) в (7.4), найдем

                                         .

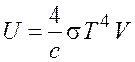Используя формулу (7.1), получим теплоемкость

                               .

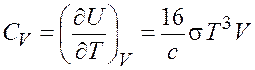Произведем расчет:

  .

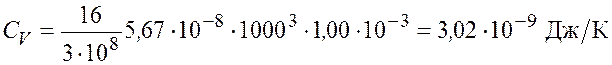Используя формулу (7.2), получим энтропию

              .

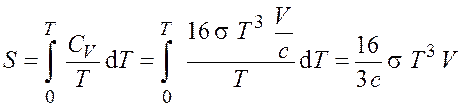Произведем расчет:

.

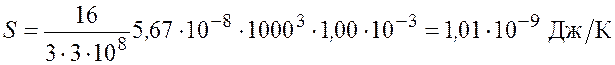Ответ: ; .

5.1.5. Задачи для решения на практических
занятиях

1. Черное тело имеет температуру 500 К. Какова будет температура тела, если в результате нагревания поток излучения увеличился в пять раз?

2. Во сколько раз увеличатся мощность излучения абсолютно черного тела и его температура, если максимум спектральной плотности энергетической светимости переместится от 700 до 600 нм?

3. Температура вольфрамовой спирали в 25-ваттной лампочке 2450 К. Отношение ее энергетической светимости к энергетической светимости абсолютно черного тела при данной температуре составляет 0,3. Найти площадь излучающей поверхности спирали. Считать, что после установления равновесия вся выделяющаяся в спирали теплота теряется в результате излучения.

4. Диаметр вольфрамовой проволоки в нити накала электрической лампочки 0,300 мм; длина проволоки 9,00 см. При включении в сеть напряжением 220 В через лампочку течет ток силой 300 мА. Найти температуру спирали, считая, что вся выделяющаяся в нити теплота теряется в виде излучения. Коэффициент черноты вольфрама равен 0,310.

5.1.6. Номера задач для самостоятельной работы студентов

1.2; 1.4; 1.10; 1.13; 1.16; 1.17; 1.19; 1.22; 1.26. [8]