Для упрощения пренебрегаем теплопритоком через изоляцию из окружающей среды.
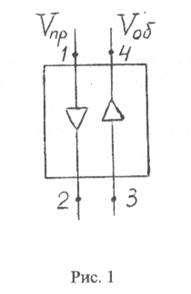
Рис. 1
2. Задается перепад температур на верхнем (теплом) конце теплообменника между прямым и обратным потоками ΔТнед = Т1 – Т4. Этот перепад температур связан с потерями от недорекуперации; он возникает в связи с конечными размерами теплопередающей поверхности аппарата, в силу чего передача тепловой энергии от одного потока к другому может происходить лишь при определенной разности температур между ними. В результате обратный поток выходит из теплообменника недогретым до температуры Т1 на величину ΔТнед. Это снижает общую тепловую нагрузку на аппарат. Рекомендуемая величина ΔТнед = 10 – 15 К.
3. Из теплового баланса теплообменника находится состояние прямого потока на выходе из аппарата (точка 2), а также тепловая нагрузка Q, кВт:
,
где
и 
–
секундные объемные расходы потоков, отнесенные к нормальным условиям (рн
= 0,1 МПа, Тн = 273 К); 
и 
– соответственно плотности прямого и обратного потоков при нормальных
условиях, кг/м3; i1, i2, i3, i4, – энтальпии потоков по
табличным данным [4], кДж/кг.*
4. Определение средней разности температур между потоками ΔТср.
При решении этой задачи надо учитывать зависимость теплоемкости потоков от изменения их температуры в процессе теплообмена. Обычно теплоемкость гелия в диапазоне используемых в криогенных циклах давлений меняется незначительно. В этом случае ограничиваются определением средней логарифмической разности температур
,
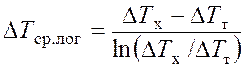где DТх = Т2 – Т3, DТт = DТнед = Т1 – Т4.
Для других теплоносителей в том случае, если теплоемкость хотя бы одного из потоков в процессе теплообмена меняется более чем на 10 %, температурный напор следует определять как среднеинтегральный методом графического интегрирования. Этот метод изложен в [1], [2], [5]. Косвенным показателем изменения теплоемкости является отношение DТх / DТт. Если величина этого отношения больше двух, следует находить среднеинтегральную разность по формуле
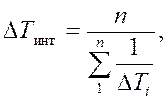
где n – число участков, на которое разбивается по высоте теплообменник, а DТi – средний перепад температур между потоками на i-м участке.
5. По справочным данным [4] определяются теплофизические параметры потоков при заданных давлениях и средних температурах:
; 
.
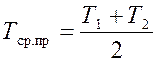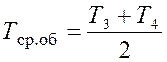К таким параметрам относятся удельный объем v,
м3/кг; плотность 
, кг/м3;
теплопроводность l, Вт/(м×К); вязкость h, Па×с; удельная теплоемкость cр, кДж/(кг×К).
6. Выбираются трубки, которыми осуществляется намотка. При этом можно воспользоваться рекомендациями в соответствии с табл. 4.2 [1] и следующими за этой таблицей пояснениями.
7. Задается массовая скорость потоков wпр и wоб в зависимости от давления и рода газа [1, с. 295].
8. Вычисляется площадь сечения трубки, м2:
и число трубок n по формуле
,
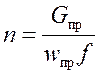где 
, кг/с; wпр – массовая скорость прямого
потока кг/(м2×с).
Полученное значение n округляется до целого n*.
Если при этом скорость 
изменится менее чем на 2 %,
корректировку скорости wпр
производить не следует. В противном случае следует уточнить
.
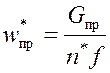9. Определяется линейная скорость газа в трубках, м/с,
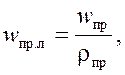
где rпр – плотность газа в трубках при Тср.пр и pпр.
10. Линейная скорость обратного потока
,
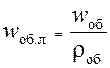где rоб – плотность газа в межтрубном пространстве при Tср.об и pоб.
11. Средняя площадь сечения свободного объема (Fс.о) в межтрубном пространстве
,
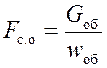где
, кг/с.
12. Площадь поперечного (фронтального) сечения межтрубного пространства для данного типа навивки и для выбранных трубок определяется в м2, по формуле
,
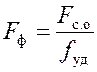где fуд = Fс.о / Fф – удельная площадь свободного сечения навивки может быть определена из табл. 4.2 [1].
13. Выбирается диаметр сердечника в пределах
Dc = (10 … 20) dн.
14. Наружный диаметр навивки, м
.
15. Далее
определяются коэффициенты теплоотдачи для прямого и обратного потоков 
и 
в следующей
последовательности:
, 
;
,
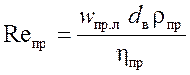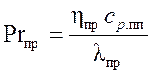где Re, Pr, Nu – критерии Рейнольдса, Прандтля и Нуссельта.
Здесь Rср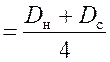 
; 
, Вт/(м2·К).
,
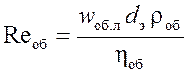где dэ – эквивалентный диаметр. Он берется из табл. 4.2 [1];
.
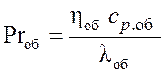Фактор теплоотдачи Кольборна
.
Эти зависимости позволяют определить число Стентона St и затем коэффициент теплоотдачи для обратного потока aоб = St wоб cр.об, Вт/(м2 × К).
16. Определяется коэффициент теплопередачи без учета термического сопротивления стенки и при КПД ребра hр = 1 (вследствие его малой длины), Вт/м2 × К
.
Здесь индексы 1 и 2 относятся соответственно к внутренней и наружной поверхностям трубки. Отношение F1 / F2 определяется по таблице 4.2 [1].
17. Площадь поверхности теплообмена в м2
.
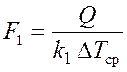18. Средняя длина трубок с 20 %-м запасом, м
.
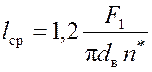19. Шаг в осевом направлении t2 = dн + 1,5dп, мм; шаг в радиальном направлении t1 = 0,866 t2, мм. Диаметр проволоки dп выбирается из табл. 4.2 [1].
20. Расчетное число слоев навивки определяется из зависимости
.
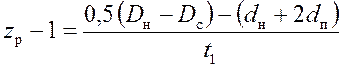Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.