


Геометрическая модель объекта криоконсервации.
Для моделирования процесса переноса теплоты необходимо принять упрощенное геометрическое строение объекта замораживания.
На первом этапе пренебрегаем тепловыми потоками вдоль оси симметрии образца; рассматриваем одномерную задачу в радиальной системе координат (считаем, что в плоскости перпендикулярной, нормальной оси симметрии все процессы симметричны, а размеры объекта позволяют нам пренебречь терлопритоками вдоль его оси). Геометрическая модель объекта приведена на рис. 1.
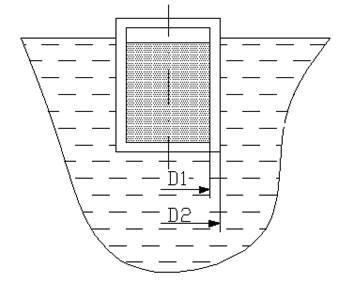 |
рис.1. Геометрическая модель объекта.
В соответствии с моделью тепловой поток из центра ампулы движется к перифирии.
D1=8 мм; D2=10 мм;
Конвективный теплообмен между поверхностью тела и теплооносителем.
В ходе процедуры криоконсервации поверхность ампулы с биопрепаратом омывается потоком теплоносителя перемещающегося от устройства подачи к устройству отвода. Движение теплоносителя побуждается незначительным перепадом давления вдоль оси движения потока, который формируется при работе блока подготовки теплоносителя [ ].
Перенос теплоты от поверхности ампулы в поток теплоносителя с достаточной для качественного анализа процесса нестационарного теплообмена точностью можно описывать уравнениями теплового подобия разработанными небиологических объектов.
Для упрощения математического описания процесса отвода теплоты можно принять следующие допущения:
- поток теплоносителя полагаем потоком несжимаемой ньютоновской жидкости;
- скорость потока вдали от твердой поверхности сохраняет постоянное значение;
- поток изотермичен , т.е. не учитываются изменения температуры газа связанные с подводом теплоты от объекта криовоздействия.
В условиях взаимодействия газового потока с поверхностью твердого тела возникает эффект «прилипания» ньютоновской жидкости к твердой поверхности и в непосредственной близости от нее, в тонком пристенном слое, возникают большие перепады скорости.
Принято [ ] условно разделять поток на две зоны: тонкий пристенный (пограничный) слой и основной, или невозмущенный, поток, в котором силой
трения можно пренебречь.
Динамическим пограничным слоем называется тонкий пристенный слой, в котором проявляются силы вязкого трения, а скорость изменяется от нуля (вблизи стенки) до скорости невозмущенного потока (на внешней границе пограничного слоя).
Как показал Г. Н. Кружилин (1936 г.), в процессе теплоотдачи температурное поле у стенки приблизительно аналогично полю скоростей, т. е. изменение температуры газа от стенки до температуры невозмущенного потока происходит в тепловом пограничном слое.
Толщина теплового пограничного слоя при ламинарном режиме движения газа зависит от толщины динамического пограничного слоя и свойств жидкости, характеризуемых критерием Рr Г. Н. Кружилиным было установлено следующее соотношение между названными величинами:
dт= dт · (Pr)-1/3 . (2.1)
Выражение (2.1) показывает, что при Pr =1 толщина теплового пограничного слоя равна толщине динамического пограничного слоя. Условие Pr =1 является условием аналогии процессов передачи теплоты и количества движения в ламинарном пограничном слое, при этом поля безразмерных скоростей и температуру у стенки становятся тождественными.
Значения критерия Pr близки к единице для большинства газов, например, для воздуха Pr=0,7. Для большинства капельных жидкостей Pr >1, и, следовательно, для них тепловой пограничный слой тоньше динамического.
С учетом принятых допущений для оценки интенсивности теплоотдачи при криоконсервационном воздействии на тело пациента можно воспользоваться следующим безразмерным уравнением [ ]:
Nu l =0.66· Re l0.55Pr ж 0.33· (Pr ж/ Pr с) 0.25. (2.2)
Индекс l у критериев Рейнольдса и Нуссельта означает, что в качестве характерного размера принята длина твердого тела вдоль оси движения потока; индекс же означает, что в качестве определяющей здесь принята температура жидкости вдали от стенки (т. е. температура невозмущенного потока).
Выражение (2.2) позволяет рассчитывать интенсивность отвода теплоты с поверхности кожи по известным значениям моделируемых факторов и является основой моделирования в численных экспериментах направленных на оценку влияния физических факторов криоконсервационного воздействия
( температуры и скорости теплоносителя).
Так как речь идет о жидких препаратах, то возможно проявление конвективных явлений. Экспериментальные наблюдения за замораживаемым объектом показали, что глицериносодержащие композиции при температуре 2 ºС мало склонны к перемешиванию, а при отрицательных температурах практически не склонны к перемешиванию. Поэтому примем допущение: конвективный перенос теплоты отсутствует. Моделируемый объект рассматривается как колоидная среда с теплопроводностью указанной в таблице, помещенная в твердую оболочку из полимерного материала. В такой постановке задача сводится к математическому моделированию процесса нестационарной теплопроводности в объекте омываемым конвективным током.
В соответствии с выбранной темой дипломной работы исследуются процессы замораживания жидких препаратов в объектах хранения. Чтобы исключить ошибки связанные с неполным учетом теплопроводности при математическом описании контейнера с жидкостью имеет большое значение выбор числа моделируемых точек в соответствии с толщиной стенки. Обязательным условием для достоверного моделирования является то, что стенка любой толщины должна разбиваться не менее чем на пять моделируемых участков. Связано это с тем, что при более крупном разбиении термическое сопротивление стенки становится равным нулю, так как в соответствии с принятыми допущениями в пределах одного элемента теплопроводность бесконечна. Поэтому в программном модуле предусмотрен автоматический выбор числа шага разбиения таким образом, чтобы в оболочке помещалось не менее пяти участков. Программа при запуске оценивает разность диаметров; она делится методом целочисленного деления на пять и определяется шаг. После этого высчитывается количество всех элементов массива, на которые разбивается моделируемый объект. Поэтому для крупных объектов с тонкой стенкой число моделируемых объектов может достигать 150 и выше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.