Свободное движение газа-теплоносителя возникает за счет неоднородности распределения гравитационных сил, которые учитываются уравнением движения [2]. Из-за подвода теплоты от поверхности объекта КВ однородность поля температур газа нарушается, возникает перепад плотностей и разность гравитационных сил, представляющих собой архимедову силу. Теплоотдача от объекта КВ определяется свободным гравитационным движением газа. Учитывая геометрию объекта и соотношение между толщиной оболочки ∆x и высотой объекта ∆y, для анализа свободного движения теплоносителя вокруг объекта охлаждения можно воспользоваться выражениями, рекомендованными для описания процесса охлаждения плоской вертикальной пластины. Свободное движение теплоносителя может быть как ламинарным, так и турбулентным.
В любом случае у поверхности тела находится ламинарный слой газа, где перенос теплоты обеспечивается теплопроводностью, поэтому интенсивность отвода теплоты от поверхности зависит от толщины пограничного слоя. Толщина ламинарного слоя δ связана с вертикальной координатой х выражением:
,
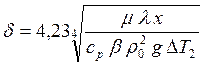(4)
где 
– ;
– коэффициент теплопередачи ;
–;
– теплоемкость;
–;
–плотность;
–ускорение свободного падения;
–градиент температур между объектом
охлаждения и газом.
Теплопроводность газа и толщина пограничного слоя определяет
величину коэффициента теплоотдачи при естественной конвекции:
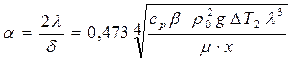(5)
Полученное выражение приводится к безразмерному виду и называется критерием Нуссельта:
, (6)
где Grx – число Грасгофа, Pr– критерий Прандтля;
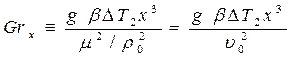, (7)
где
–кинематическая
вязкость газа.
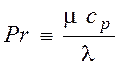. (8)
В инженерных расчетах используют средние значения температур и коэффициента теплоотдачи. Средняя теплоотдача вертикальной поверхности с постоянной температурой в условиях ламинарного течения описывается выражением:
(9)
Коэффициенты пропорциональности в формулах (6) и (9) получены с использованием результатов физических исследований.
Для расчета местных коэффициентов теплоотдачи при свободном ламинарном течении вдоль вертикальных стенок рекомендовано выражение [2]:
(10)
Формула (10) получена при условии постоянства теплового потока с поверхности. Расчетная формула для среднего коэффициента теплоотдачи в ламинарном режиме:
(11)
Эта формула справедлива при условии: 103 < Grжх· Prж < 109.
При развитом турбулентном течении газа, которое наступает при числахGrжх· Prж> 6·1010, местные коэффициенты теплоотдачи вычисляются по формуле
(12)
При развитом турбулентном течении коэффициент теплоотдачи не зависит от линейного размера и, следовательно, местный коэффициент теплоотдачи равен среднему.
Переходной режим имеет место примерно при 109 < Grжх· Prж < 6∙1010. В среднем теплоотдача при переходном режиме возрастает от значения, соответствующего ламинарному течению, до значения, соответствующего турбулентному движению газа. Наибольшее и наименьшее значения коэффициента теплоотдачи в переходной области можно определить соответственно по уравнениям (10) и (12).
Выражение для расчета критерия Нуссельта представляется в общем виде:
(14)
Для газов Prж/Prc ≈ 1, поэтому Nu= A(Gr·Prж)n
Значения констант А и n в зависимости от режима течения сведены в табл.1.
Таблица 1
Значение констант для вычисления критерия Нуссельта
с учетом характера течения газового потока
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.