Разработка криотерапевтического комплекса по индивидуальным параметрам объекта воздействия, страница 2

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА ОХЛАЖДЕНИЯ

Для описания переноса теплоты через слои охлажденного объекта используем уравнение энергии в одномерном виде 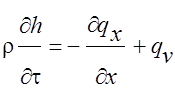[1]:

                                                ,                                                    (1)

где   h – энтальпия (теплосодержание) материала, образующего слой, q_х – тепловой поток вдоль координаты х, q_v –теплота, выделяемая внутренними источниками в единице объема.

При замене в уравнении (1) производных конечно–разностными приближениями получено:

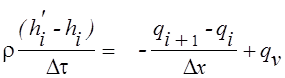                                   ,                    (2)

где  h^′_i  –энтальпия в  ί-точке в момент времени τ+∆τ, q_i, q_i+1 – соответственно подвод теплоты от узловых точек.

Решая  уравнение (2) относительно h^′_i  , получаем: 

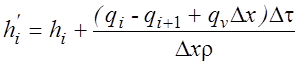        .                  (3)

1.3. Расчет индивидуальных характеристик объекта  криотерапевтического воздействия.

Толщина оболочки определяется по известному весу объекту криовоздействия. Вес оболочки:

 кг.

Средняя площадь наружной поверхности тела  м².

Толщина оболочки:

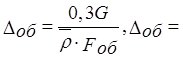0,0164 м.

Толщина эпителиального слоя: 0,00205 м.

Толщина жирового слоя: 0,01025 м.

Окончательно принимаем:

 2 мм,  10,5 мм.

1.4. Порядок выполнения исследований

Исследования выполняются методом вычислительного эксперимента. В эксперименте используются алгоритмы и программные продукты, разработанные при выполнении предыдущих работ курса, в частности методы расчета коэффициента конвективной теплоотдачи, математическая модель оболочки человеческого тела, условия однозначности.

Вычислительный эксперимент сводится к последовательному выполнению численного моделирования процесса конвективного охлаждения объекта ОКВ при 10 значениях температуры газа Т₁. Схема процесса охлаждения приведена на рис.1.

Рис.1  Схема эксперимента по оптимизации температурного режима охлаждения в условиях естественной конвекции.

Таблица 1

Результаты уточняющего численного эксперимента.

По результатам численного эксперимента строим диаграмму изменения величины теплового потока

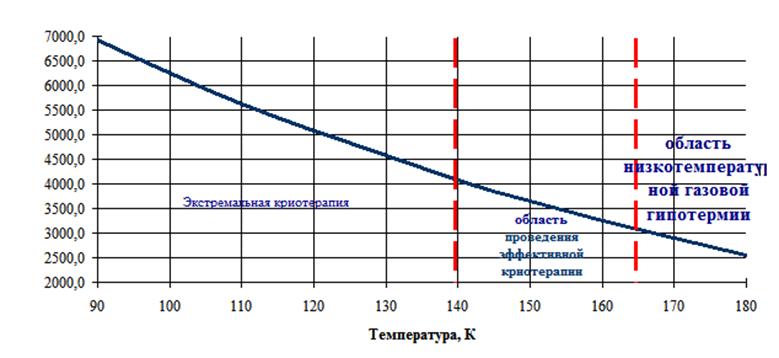
Рис. 2. Изменения плотности теплового потока с поверхности объекта охлаждения.

По результатам численного эксперимента строим диаграмму изменения температуры поверхности ;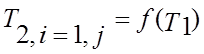

Наряду с тепловыми характеристиками следует построить и рассчитать параметры, характеризующие стимулирующее действие ОКВ: