Групповые и индивидуальные криотерапевтические комплексы, страница 5

Перенос теплоты определяется конвективными процессами на наружной и внутренней поверхности теплового ограждения, для построения математической модели можно воспользоваться  физической моделью элемента изоляции  (см. рис.3.1.1).

 

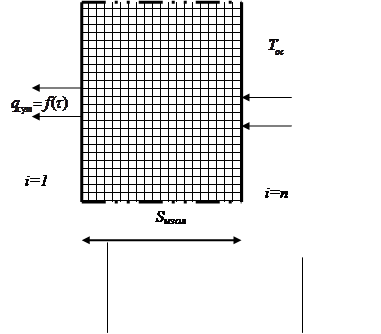
Рис. 3.1.1 Схема переноса теплоты через тепловое ограждение.

На рис.3.1.1  представлен фрагмент теплового ограждения процедурной кабины с произвольной толщиной S_изол.

Изменение температуры теплового ограждения под действием нестационарного переноса теплоты описывается одномерным уравнением энергии:

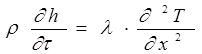
Применение одномерного уравнения энергии оправдано тем, что размеры моделируемого объекта (высота и толщина изоляции) отличаются на порядок. Это позволяет пренебречь переносом теплоты вдоль высоты теплоизоляционного ограждения.

 Температура наружной стенки ограждения   почти постоянна  и близка к температуре окружающей среды.

     Температура внутренней поверхности ограждения изменяется во времени:

T_3,i=1   = f ( t)      

Для любого горизонтального сечения  изоляции можно записать:

Вычисляется приращение теплосодержания в элементарных точках сетки разбиения. Значения температур получают по расчетным значениям энтальпий. В уравнении энэргии заменим производными разностными приближениями

 

где  h_i ,  h_i^¢ – соответственно текущее и последующее значение энтальпии в ί-точке;  q_i+1 , q_i-1 – соответственно тепловой поток от предыдущей и последующей точек; V  –  объем вещества, отнесенный  к       ί-точке.

Энергия подводимая к элементарной  точке теплопроводностью определяется как : ,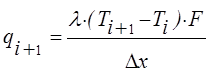

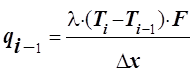
где  Dx  – расстояние между точками (шаг разбиения); F – площадь, через которую переносится теплота.

Граничные условия:

  q_i‑1 = a_вн×F×( T₁ - T_i ) ,

где  a_вн  – коэффициент теплоотдачи; T₁  – температура  теплоотводящей среды.

К наружному слою (i = n_i)  теплота подводится атмосферным воздухом, температура воздуха =293 К:

q_i+1 = × F×( T_ос - T_i )

Начальные условия можно представить в виде:

при t = 0             T_3i  = T_ос

Вычисляя значения энтальпии на  следующем временном слое:

                               

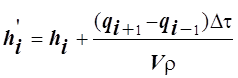
и по ним определяем  соответствующие значения температуры   T_i^' =f ( h_i^'

 Алгоритм вычисления реализован в программе Word Excel .

 Для получения достоверных результатов перечисленные величины рассчитываются для каждой точки координатной сетки (x, t ).  

 3.2. Индивидуальное задание по изоляции

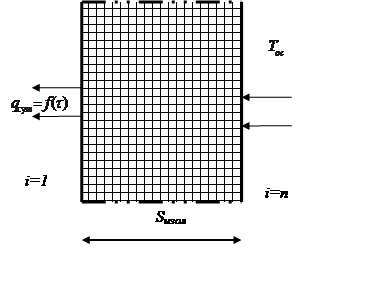
   Тепловое ограждение криотерапевтического комплекса работает в квазистационарных условиях.  Хотя средняя температура в кабине условно постоянна, на самом деле при входе и выходе пациентов в кабину наблюдается скачок температуры на 70-80 К, что сказывается на тепловом обмене между изоляцией и газом. Периодически направление тепловых потоков меняется: то изоляция является источником теплоты, то газ. Эти процессы сказываются на работе установки. Для того, чтобы изучить это явление, используется метод математического моделирования. Процессы, протекающие в  тепловой изоляции при колебании температуры газа,  поясняются тепловой схемой, которая приведена на рисунке 3.2.1.

 

 

                         Рис. 3.2.1

      Изоляционный материал, например пенополистирол, толщиной S, находится в тепловом контакте с окружающей средой в точке с i=n и с криогенным теплоносителем, температура которого Т1 меняется во времени. В результате через изоляционную конструкцию движется тепловой поток, который частично поступает из окружающей среды, а частично связан с теплоаккомулируещей способностью самой изоляции.  Для моделирования процесса изоляция разбивается на условные n участков, для которых составляется тепловой баланс, что позволяет нам рассчитать  изменение температуры за время одного процедурного цикла.

       Характер изменений, которые претерпевает температура во время процедурного цикла, поясняется графиком, приведенным на рисунке 3.2.2. До начала процедурно цикла за счет работы системы криостатирования температура в кабине пациента доводится до номинального уровня, например 130 К (этап I). В момент входа пациента происходит смешение газа в кабине с газом из шлюза, где температура газа гораздо выше.