Расчет начального значения периодической составляющей тока трехфазного КЗ в заданной точке «К» схемы, ударного тока и его действующего значения, страница 6

При расчете тока трехфазного КЗ аналитическим методом были определены результирующие сопротивление Х⁽³⁾_рез и ЭДС Е⁽³⁾_рез.

Х_1рез= Х⁽³⁾_рез=0,74,

Е_рез1= Е⁽³⁾_рез=1,04.

5.2 Расчет результирующего сопротивления обратной последовательности

Схема обратной последовательности по своей конфигурации является полной копией схемы прямой последовательности, только ЭДС всех генерирующих элементов в ней равны нулю, а генераторы вводятся в нее сопротивлениями обратной последовательности, отличными от сопротивлений прямой последовательности. Все остальные элементы вводятся теми же сопротивлениями, что и в схему прямой последовательности.

Индуктивное сопротивление генератора обратной последовательности Х_*2Гб в относительных единицах, приведенное к базисным условиям, определяется по формуле:

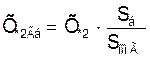,                                                                 (5.3)
где Х_*2 – сопротивление обратной последовательности в относительных единицах.

В приближенных расчетах принимают для генераторов и входящих в схему нагрузок Х₂=Х₁. это освобождает от составления схемы замещения обратной последовательности и позволяет принимать Х_1рез= Х_2рез.

5.3 Определение симметричных составляющих фазных токов и напряжений двухфазного КЗ

Для упрощения место повреждения относится на холостое ответвление, поэтому токи в фазах этого ответвления можно считать токами КЗ. За положительное направление токов принимается их направление к точке КЗ.

Двухфазное короткое замыкание между фазами В и С можно записать граничными условиями:

 - так как КЗ отнесено на холостое ответвление;

 - поскольку система токов уравновешенная  и .

 - так как линия имеет общую точку КЗ.

При таком виде повреждения токи нулевой последовательности отсутствуют ; .

Если фазу А принять за особую (расчетную), то при использовании формул симметричных составляющих достаточно вычислить значение одной фазы – все остальные можно определить через оператор.

Токи прямой последовательности в фазах:

;

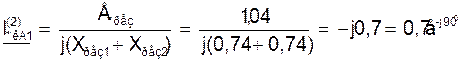кА;

кА;

кА.

Токи обратной и нулевой последовательности в фазах:

кА;

кА;

кА;

Ток КЗ а аварийных фазах:

кА;

кА.

Напряжения симметричных составляющих прямой и обратной последовательностей:

кВ;

кВ;

кВ;

кВ;

кВ;

кВ.

Фазные напряжения в месте КЗ:

кВ;

кВ.

5.4 Векторные диаграммы токов и напряжений двухфазного КЗ

Векторные диаграммы токов и напряжений построены в соответствии с соотношениями, полученными в пункте 5.3.

Фазные токи находят как геометрическую сумму симметричных составляющих соответствующих фаз, правильность построения которых подтверждается формулами.

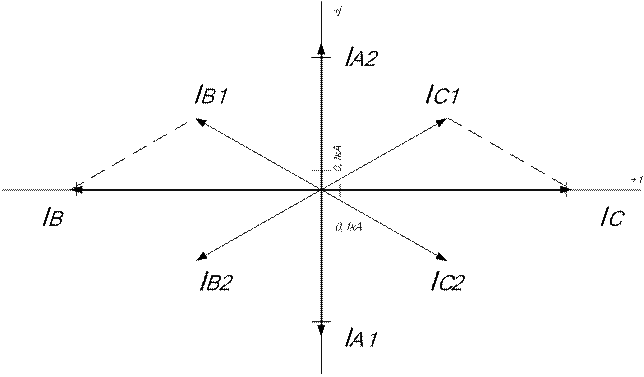
Рисунок 5.1 – Векторная диаграмма токов в месте двухфазного КЗ

                       

Рисунок 5.2 – Векторная диаграмма напряжений в месте двухфазного КЗ