Расчет сложной линейной цепи постоянного тока

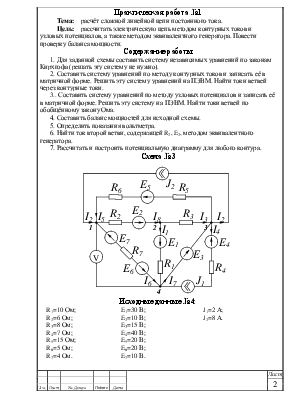
Практическая работа №1

          Тема:    расчёт сложной линейной цепи постоянного тока.

          Цель:    рассчитать электрическую цепь методом контурных токов и узловых потенциалов, а также методом эквивалентного генератора. Повести проверку баланса мощности.

Содержание работы

1. Для заданной схемы составить систему независимых уравнений по законам Кирхгофа (решать эту систему не нужно).

2. Составить систему уравнений по методу контурных токов и записать её в матричной форме. Решить эту систему уравнений на ПЭВМ. Найти токи ветвей через контурные токи.

3.. Составить систему уравнений по методу узловых потенциалов и записать её в матрич­ной форме. Решить эту систему на ПЭВМ. Найти токи ветвей по обобщённому закону Ома.

4. Составить баланс мощностей для исходной схемы.

5. Определить показания вольтметра.

6. Найти ток второй ветви, содержащей R₂, E₂, методом эквивалентного генератора.

7. Рассчитать и построить потенциальную диаграмму для любого контура.

Схема№3

Исходные данные №4:

    R₁=10 Ом;                          E₁=30 В;                                  J₁=2 А;

    R₂=6 Ом;                            E₂=10 В;                                  J₂=8 А.

    R₃=8 Ом;                            E₃=15 В;

    R₄=7 Ом;                            E₄=40 В;

    R₅=15 Ом;                          E₅=20 В;

    R₆=5 Ом;                            E₆=20 В;

    R₇=4 Ом.                            E₇=10 В.

1. Система независимых уравнений по законам Кирхгофа.

Граф

Число ветвей  в=6

Число узлов   у=4

N_мус=в=6

N_1зк=у–1=3

N_2зк=в–(у–1)=3

∑I_i=0                      ∑R_i∙I_i=∑E_i

     – I₂– I₅+ I₆+ I₈=0

     – I₈+ I₃+ I₁=0

     I₅+ I₂+ I₄– I₇– I₃=0

     R₃∙I₂– R₂∙I₈–  (R₅+R₆)∙I₅=–E₂– E₅

     R₁∙I₁– R₇∙I₆+ R₂∙I₈= E₁– E₆+ E₇+ E₂

     – R₁∙I₁+ R₃∙I₃=– E₃– E₁

Учитывая, что I₂= J₂ и I₄=J₁ получаем уравнение с шестью неизвеснымы!

2. Система уравнений по методу контурных токов.

N_мкт= к= 3

Дерево графа:

         Все контурные токи протекают почасовой стрелки.

     (R₃+ R₂+ R₆+ R₅)∙I₁₁– R₂∙I₂₂– R₃∙I₃₃= 0∙I₄₄– (R₅+R₆) ∙I₅₅– E₂– E₅

     – R₂∙I₁₁+ (R₁+ R₇+ R₂) ∙I₂₂– R₁∙I₃₃= 0∙I₄₄+ 0∙I₅₅+ E₁– E₆+ E₇+ E₂

–  R₃∙I₁₁– R₁∙I₂₂+ (R₁+ R₃) ∙I₃₃= 0∙I₄₄+ 0∙I₅₅– E₃– E₁

Общая запись: | R | × | I | = | E |

          34  -6  -8               I₁₁                -190

          -6  20  -10    X       I₂₂        =      30

          -8  -10  18             I₃₃                -45

Решая уравнения на ПЕВМ, рассматривая матрицы, получаем:

I₁₁= Δ₁/Δ=– 9,015 A

I₂₂= Δ₂/Δ=–6,173 A

I₃₃= Δ₃/Δ=– 9,936 A

I₁= I₂₂– I₃₃= 3,763 A

I₃= I₃₃– I₂₂=– 0,921 A

I₅=– I₁₁– J₂= 1,015 A

I₆=– I₂₂= 6,173

I₇= J₁– I₃₃= 11,936 A

I₈= I₂₂– I₁₁= 2,843 A

Проверяем путём подстановки полученных значений в уравнения состояния по 2^ому закону  Кирхгофа.

3. Система уравнений по методу узловых потенциалов.

Заземляем φ₄= 0. Тогда φ₃ = E₃= 15 В. Запишем уравнения для оставшихся потенциалов, с учётом  φ₃.

      φ₁∙ –  φ₂∙ =+ – + J₂

     – φ₁∙+ φ₂∙= + –

Общая запись: | G | × | φ | = | I |

          0,46       –0,167              φ₁               5,583

                                        X                =

          –0,167   0,392                φ₂               0,542

Решая уравнения на ПЕВМ, рассматривая матрицы, получаем:

φ₁= Δ₁/Δ= 14,691 В

φ₂= Δ₁/Δ= 7,634 В

I₁= = 3,763 А

I₃==– 0,921 А

I₅== 1,015 А

I₆== 6,173 А

I₈== 2,843 А

Ток I₇ находим по 2^ому закону Кирхгофа:

I₇=J₁+ I₆+ I₁= 11,936 А

Проверяем путём подстановки полученных значений в уравнения состояния по 1^ому закону  Кирхгофа. Значения токов должны совпадать с полученными токами, найденными методом контурных токов.

4. Баланс мощности.

Балан мощности заключается в том, что вырабатываемая мощность всех источников равна мощности всех потребителей. Другими словами:

∑E_i∙I_i+ ∑U_Ji∙J_i= ∑R_i∙I_i²

Сначала находим напряжения на ист. тока:

U_J1= E₅+ I₅∙(R₅+ R₆)=39 В

U_J2= E₄– E₃+ J₁∙R₄=– 0,309 В

P_ист= ∑E_i∙I_i+ ∑U_Ji∙J_i= E₁∙I₁+ E₂∙I₈+ E₃∙I₇– E₄∙I₄+ E₅∙I₅+ (E₆+E₇)∙I₆+U_J1∙J₁+ U_J2∙J₂= 397,936 Вт;

P_потр= ∑R_i∙I_i²= R₁∙I₁²+ R₂∙I₈²+ R₃∙I₃²+ R₄∙I₄²+ (R₅+R₆)∙I₅²+ R₇∙I₆²= 397,936 Вт;

Т. к. P_ист=P_потр, то баланс мощности выполняется и это свидетельствует о том, что всё сделано правильно.

5. Найти показания вольтметра.

Из схемы очевидно, что напряжение на вольтметре определяется между φ₄ и φ₃.

U_V= φ₁– φ₄= φ₁= 14,691 В.

6. Метод эквивалентного генератора.

Чтобы найти силу тока на R₂ E₂ методом эквивалентного генератора надо найти E_экв, которое равно U_ХХ на этом элементе и R_экв, которое получается путём размыкания ист. тока и обнуления ист. ЕДС, т. е. из активной схемы получаем пассивную. А сила тока равна I=.

E_экв= U_АБ= φ_А– φ_Б= φ₁– φ₂

Перепишем МУП без R₂ и E₂.

      φ₁∙ =+ + J₂

      φ₂∙= –

E_экв== 29,167 В

Найдём R_экв заменяя последовательные и параллельные R на R`_экв:

R_экв==7,778 Ом.

Теперь найдём I₈:

I₈===2,843 А

7. Потенциальная диаграмма.

Обойдём все узлы от последнего к первому:

Заземляем φ₁= 0 В

φ₂= φ₁+ E₃= 15 В

φ₃= φ₂+ R₃∙I₃= 7,634 В

φ₄= φ₃– E₂=– 2,366 В

φ₅= φ₄+ R₂∙I₈= 14,691 В

φ₆= φ₅– E₇= 4,691 В

φ₇= φ₆+ R₇∙I₆=– 20 В

φ₁= φ₇+ E₆=0 В

r₁= 0 Ом

r₂= r₁= 0 Ом

r₃= r₂+ R₃= 8 Ом

r₄= r₃= 8 Ом

r₅= r₄+ R₂= 14 Ом

                                                                                        r₆= r₅= 14 Ом

                                                                                        r₇= r₆+ R₇= 18 Ом

                                                                                        r₈= r₇= 18 Ом

Потенциальная диаграмма