ТЕМА : Синтаксис класса
СРОК СДАЧИ : 5 неделя
ЦЕЛЬ РАБОТЫ : Изучение синтаксиса класса
ТЕОРЕТИЧЕСКИЕ ЗНАНИЯ : Синтаксис структуры. Выделение памяти под элемент структуры. Обращение к элементу структуры. Использование структуры в качестве параметра функции. Массивы структур. Использование массива структур в качестве параметра функции.
Составьте программу, которая решает поставленную в вашем варианте задачу. Программа должна:
Ø представлять собой консольное приложение
Ø содержать русско-язычный интерфейс
Ø содержать ввод исходных данных с клавиатуры или исходные данные должны быть заданны в качестве начальных значений переменных
Ø отображать сведения о назначении и возможностях программы
Ø отображать сведения об авторе программы
Ø выводить результаты расчётов на экран
Ø содержать запрос о продолжении работы
Ø содержать в коде необходимые пояснения
Ø код программы должен быть оформлен в виде класса, функции которого вызываются из функции main
Задание |
|
Вариант 1. Заданы координаты вершин четырёхугольника. Определить является ли этот четырёхугольник выпуклым |
|
Вариант 2. Заданы координаты вершин треугольника и координаты точки. Определить, расположена ли точка внутри треугольника или снаружи |
|
Вариант 3. Заданы координаты двух вершин правильного треугольника. Определить координаты третьей вершины (два решения) и его площадь |
|
Вариант 4. Заданы координаты двух вершин основания равнобедренного треугольника и его высота. Определить координаты третьей вершины (два решения), его площадь и углы треугольника |
|
Вариант 5. Заданы координаты вершины, основания высоты и площадь равнобедренного треугольника. Определить координаты двух других вершин и углы треугольника |
|
Вариант 6. Заданы координаты прямого угла, вершины прямоугольного треугольника и длина его гипотенузы. Определить координаты третьей вершины (два решения), длину катетов, площадь и углы треугольника |
|
Вариант 7. Заданы координаты прямого угла, вершины прямоугольного треугольника и длина его катета. Определить координаты третьей вершины (два решения), длину гипотенузы, площадь и углы треугольника |
|
Вариант 8. Заданы координаты острых углов прямоугольного треугольника и длина его катета. Определить координаты третьей вершины, длину всех сторон, площадь и углы треугольника (четыре решения) |
|
Вариант 9. Заданы координаты острых углов прямоугольного треугольника и значение острого угла. Определить координаты третьей вершины (четыре решения), длину всех сторон и площадь треугольника |
|
Вариант 10. Заданы координаты острых углов прямоугольного треугольника и значение острого угла. Определить координаты третьей вершины (четыре решения), длину всех сторон и площадь треугольника |
|
Вариант 11. Заданы координаты центра и вершины правильного треугольника. Определить координаты двух других вершин и его площадь |
|
Вариант 12. Заданы координаты центра и вершины квадрата. Определить координаты двух других вершин и его площадь |
|
Вариант 13. Заданы координаты центра и вершины пятиугольника. Определить координаты остальных вершин и его площадь |
|
Вариант 14. Заданы координаты вершины ромба, точки пересечения диагоналей и его площадь. Определить координаты остальных вершин и длину всех сторон. |
|
Вариант 15. Заданы координаты двух вершин квадрата. Определить координаты двух других вершин и его площадь (два решения) |
|
Вариант 16. Заданы координаты вершин треугольника. Определить координаты середин сторон треугольника |
|
Вариант 17. Заданы координаты середин треугольника. Определить координаты вершин треугольника |
|
Вариант 18. Заданы координаты вершин треугольника. Определить координаты точки пересечения медиан |
|
Вариант 19. Заданы координаты двух вершин треугольника и точки пересечения его медиан. Определить координаты третьей вершины треугольника |
|
Вариант 20. Заданы координаты двух смежных вершин параллелограмма и координаты точки пересечения диагоналей. Определить координаты двух других вершин параллелограмма |
|
Вариант 21. Заданы координаты трёх вершин параллелограмма. Определить координаты четвёртой вершины параллелограмма и точки пересечения его диагоналей |
|
Вариант 22. Заданы координаты двух точек, ограничивающих отрезок. Отрезок разделён на три равные части. Определить координаты точек деления. |
|
Вариант 23. Заданы координаты центра и вершины квадрата. Определить координаты двух других вершин и его площадь |
|
Вариант 24. |
|
Вариант 25. |
|
Вариант 26. |
Ø
1. Синтаксис структуры.
2. Выделение памяти под элемент структуры.
3. Обращение к элементу структуры.
4. Использование структуры в качестве параметра функции.
5. Использование структуры в качестве значения, возвращаемого функцией.
6. Массивы структур.
7. Использование массива структур в качестве параметра функции.
Проекции вектора ![]() можно
вычислить по координатам начала (точка А) и конца (точка В) использую следующую
формулу:
можно
вычислить по координатам начала (точка А) и конца (точка В) использую следующую
формулу:
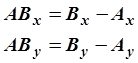
Координаты конца (точка В) вектора ![]() можно вычислить по координатам
можно вычислить по координатам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.