Ø
1. Перегрузка оператора присваивания.
2. Перегрузка бинарных операторов.
3. Перегрузка унарных операторов.
4. Перегрузка операторов ++ и --.
5. Перегрузка оператора вызова функции.
6. Перегрузка оператора преобразования типа.
Проекции вектора ![]() можно
вычислить по координатам начала (точка А) и конца (точка В) использую следующую
формулу:
можно
вычислить по координатам начала (точка А) и конца (точка В) использую следующую
формулу:
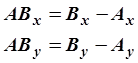
Координаты конца (точка В) вектора ![]() можно вычислить по координатам начала
(точка А) и проекциям вектора АВ использую следующую формулу:
можно вычислить по координатам начала
(точка А) и проекциям вектора АВ использую следующую формулу:
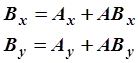
Модуль вектора ![]() (длину)
можно вычислить по теореме Пифагора:
(длину)
можно вычислить по теореме Пифагора:
![]()
Расстояние D между двумя точка A и B можно вычислить по теореме Пифагора:
![]()
Площадь S треугольника со сторонами a, b и с можно вычислить по формуле Герона:
![]()
где 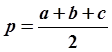
Скалярное произведение векторов ![]() и
и ![]() можно
вычислить по следующей формуле:
можно
вычислить по следующей формуле:
![]()
Угол ![]() между векторами
между векторами ![]() и
и ![]() можно
вычислить по следующей формуле:
можно
вычислить по следующей формуле:
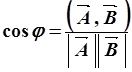
Проекции вектора ![]() ,
повёрнутого относительно вектора
,
повёрнутого относительно вектора ![]() на угол
на угол ![]() , можно вычислить по следующей формуле:
, можно вычислить по следующей формуле:
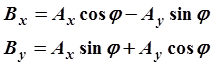
Проекции вектора ![]() ,
перпендикулярного вектору
,
перпендикулярного вектору ![]() , можно вычислить по
следующей формуле:
, можно вычислить по
следующей формуле:
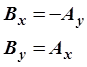
Не трудно видеть, что скалярное произведение ![]() векторов
векторов ![]() и
и ![]() в этом случае равно нулю
в этом случае равно нулю
Умножение вектора ![]() на
число К можно выполнить по следующей формуле:
на
число К можно выполнить по следующей формуле:
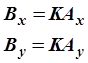
Нетрудно видеть, что вектор ![]() в К раз длиннее вектора
в К раз длиннее вектора ![]() и параллелен вектору
и параллелен вектору ![]()
Уравнение прямой ![]() ,
проходящей через точки
,
проходящей через точки ![]() и
и ![]() имеет
вид:
имеет
вид:
Ø
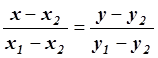
Откуда легко получить:
![]()
Следовательно:
![]()
Две прямые ![]() и
и ![]() перпендикулярны друг другу, если:
перпендикулярны друг другу, если:
![]()
Если прямая ![]() известна, то коэффициенты
известна, то коэффициенты ![]() и
и ![]() прямой
прямой ![]() можно вычислить по следующим формулам:
можно вычислить по следующим формулам:
![]()
Прямая ![]() проходит
через точку
проходит
через точку ![]() , если:
, если:
![]()
Детерминант матрицы размером 2´2 можно вычислить по следующей формуле:
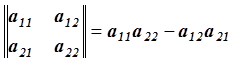
Задачу нахождения точки пересечения двух прямых на плоскости можно свести к решению двух линейных уравнений с двумя неизвестными методом Крамера:
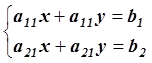
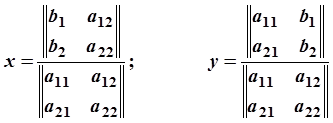
Прямая ![]() перпендикулярна
вектору
перпендикулярна
вектору ![]() с проекциями
с проекциями ![]() , если:
, если:
![]()
Прямая ![]() проходит
через точку
проходит
через точку ![]() , если:
, если:
![]()
Прямая ![]() перпендикулярна
вектору
перпендикулярна
вектору ![]() с проекциями
с проекциями ![]() , если:
, если:
![]()
Прямая ![]() проходит
через точку
проходит
через точку ![]() , если:
, если:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.