Наукова графіка в середовищі MatLab (Лабораторна робота № 1), страница 3

де x – вектор абсцис точок, y – вектор ординат, z – матриця апплікат, С – матриця кольорів точок (якщо матриця кольорів не задана, то приймається значення кольору рівне Z, тобто колір характеризує значення апплікати). Якщо вектор х містить n елементів, а вектор у – m, то матриця Z повинна мати розмір m ´ n елементів

Приклад:

3. Функція rotate3d – Включає режим інтерактивного управління місцеположенням камери. Після команди

rotate3d on

з’являється можливість за допомогою миші обертати тривимірний графік, наприклад наведемо попередній графік з іншим місцеположенням камери:

Завдання

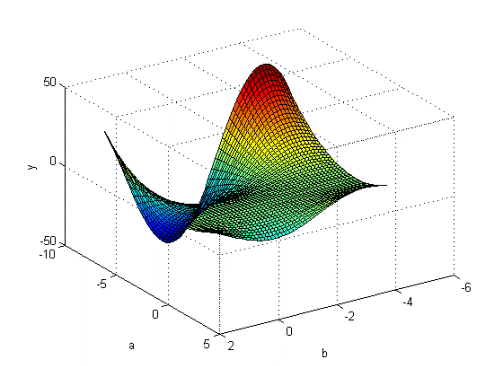
При аналізі лінійних динамічних систем управління виникає необхідність перевірки їх стійкості. Для цього необхідно побудувати годограф Михайлова, що визначається за такими формулами (для системи 4-го порядку):

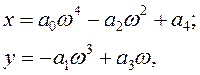
де

Для значень

на проміжку :

1. Побудувати на одній фігурі залежності  та

1.1. Встановити діапазон виводу [0 8.6 –25 20]

1.2. Включити сітку;

1.3. Додати до фігури легенду;

1.4. Встановити назви осей;

1.5. Позначити точки перетину залежностями  та осі абсцисс як w0, w1, …;

1.6. Встановити назву фігури.

2. Побудувати на окремому графіку залежність у(х)

2.1. Включити сітку;

2.2. Вказати назви осей;

2.3. Позначити текстовими коментаріями на фігурі точки  та ;

2.4. Дати назву фігурі ‘Mihaylovs Hodograph’.

3. Побудувати тривимірний графік функції згідно варіанта:

За допомогою інтерактивного режиму зміни положення камери одержати 3 проекції побудованого в попередньому пункті графіка (вигляд зверху та вигляди з двох боків).