Написання програм TRIANGLE, CHERRY і ALCHEMY (Завдання першого туру XVI Всеукраїнської олiмпiади з iнформатики), страница 2

Якщо отримати цільову речовину неможливо, єдиний рядок вихідного файлу має містити число -1.

Для наведеного прикладу вхідних даних, цільову речовину 4 можна отримати, якщо на протязі перших трьох одиниць часу провести реакцію 2, а після цього на протязі двох одиниць часу провести реакцію 3. Таким чином, за 5 одиниць часу буде отримана потрібна речовина.

Приклад вхідних та вихідних даних

ALCHEMY.DAT	ALCHEMY.SOL
4 3 1 4 8 1 1 1 4 3 1 1 2 2 3 2 2 1 3 1 4	5

XVI Всеукраїнська олімпіада з інформатики

Другий тур

Ланцюг (100 балів)

Є N шматків ланцюга, кожен i-й з яких містить L_i ланок. Можна розгинати довільні ланки та потім згинати їх знову, з’єднуючи окремі шматки.

Завдання

Напишіть програму CHAIN, що за кількістю шматків ланцюга N та кількістю ланок у шматках L_i визначає мінімальну кількість ланок яку потрібно розігнути та зігнути знову, щоб з’єднати усі шматки в один ланцюг. Ланцюг не може мати розгалужень, тобто кожна його ланка повинна бути з’єднана з двома іншими ланками (крім двох ланок з країв ланцюга, що повинні бути з’єднані лише з однією ланкою).

Вхідні дані

В першому рядку вхідного файлу CHAIN.DAT знаходиться ціле число N (2£N£10 000). В другому рядку знаходяться N цілих чисел L_i (1£L_i£1 000 000 000).

Вихідні дані

В єдиному рядку вихідного файлу CHAIN.SOL повинно знаходитися ціле число — найменша кількість ланок, яку потрібно розігнути та зігнути знову, щоб отримати один ланцюг з усіх шматків.

Приклад вхідних та вихідних даних

CHAIN.DAT	CHAIN.SOL
3 100 3 4	2

Казино (100 балів)

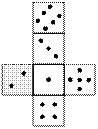У верхньому лівому куті прямокутного поля розмірами N´M розміщено гральний кубик, розворот якого зображено на малюнку. Кубик орієнтовано так, що передній грані відповідає одиниця, а зліва знаходиться грань, якій відповідає двійка. Клітини поля квадратні, їх розміри співпадають з розмірами грані кубика.

               Кубик може рухатися по полю, перегортаючись через одне з ребер, та потрапляти при цьому до сусідньої знизу, згори, праворуч або ліворуч клітини поля. Наприклад, якщо з початкового стану кубик рухається праворуч, то передньою стане грань з двійкою, а якщо вниз — то з трійкою. Кубик не може виходити за межі поля.

Завдання

Напишіть програму CASINO, що за інформацією про поле знаходить один з можливих шляхів кубика з верхнього лівого кута у нижній правий кут поля. При цьому потрібно знайти такий шлях, щоб передня грань кубика у цільовій клітині мала максимальне можливе значення. Кубик може відвідувати кожну клітину поля декілька разів.

Вхідні дані

Перший рядок вхідного файлу CASINO.DAT містить два натуральних числа N та M (2£N, M£50), що визначають висоту та ширину поля відповідно. Далі задається поле, яке представлене N рядками, кожен з яких складається з M чисел, кожне з яких дорівнює 0 або 1. У випадку, коли клітині поля відповідає число 1, кубику заборонено відвідувати дану клітину. В іншому разі ця клітина може зустрічатись у шляху кубика. Початковій клітині завжди відповідає число 0.

Вихідні дані

Перший рядок вихідного файлу CASINO.SOL повинен містити натуральне число W — довжину знайденого шляху. Далі у файлі мають знаходитися W рядків, кожен з яких задає координату клітини поля на поточному кроці. Координата являє собою пару натуральних чисел: номер рядка та номер стовпчика клітини поля.

У випадку коли шуканого шляху не існує, вихідний файл має містити рядок з числом -1.

Приклад вхідних та вихідних даних

CASINO.DAT	CASINO.SOL
3 2 0 1  0 0 0 0	3 2 1 2 2 3 2

Система рівнянь (100 балів)

Нехай k-те рівняння системи з N рівнянь має вигляд X+Y=b_k, де X=x_1k+x_2k+…+x_{k-1 k}; Y=x_{k k+1}+…+x_{k N}. Таким чином, ліва частина кожного рівняння має N-1 доданок та кожне невідоме зустрічається рівно в двох рівняннях системи.

Завдання

Напишіть програму SYSTEM, що за заданими b₁,…,b_N знаходить один з розв’язків системи, при умові що невідомі x_ij можуть набувати лише значення 0 або 1.

Вхідні дані

В першому рядку вхідного файлу SYSTEM.DAT знаходиться натуральне число — кількість тестових блоків. Кожний тестовий блок починається з рядка, який містить число N (3£N£50) — кількість рівнянь у системі. У другому рядку блока знаходиться N цілих чисел b_i (0£b_i£50).

Вихідні дані

Для кожного тестового блоку до вихідного файлу SYSTEM.SOL повинен бути записаний один з розв’язків системи: N-1 рядків, кожен k-й з яких містить N-k чисел — знайдених значень невідомих:

x₁₂  … x_1N

x₂₃  … x_2N

x₃₄  … x_3N

…

x_N-_{1 N}

Якщо система не має розв’язків для тестового блоку, у вихідний файл повинен бути записаний рядок, що містить єдине число -1.

Приклад вхідних та вихідних даних

SYSTEM.DAT	SYSTEM.SOL
2 3 1 2 3 5 3 2 3 2 2	-1 1 1 1 0 0 0 1 1 1 0