


Лабораторна робота №3
Тема: "Розробка і реалізація програм для розв’язку трансцендентних рівнянь із застосуванням циклічних та умовних операторів"
Завдання: Скласти програму для розв’язку трансцендентного рівняння методом ділення відрізка пополам.
Теоретичні відомості:
Як відомо з курсу математики, трансцендентним називається рівняння, що не може бути розв’язане в аналітичному вигляді. Наприклад, до трансцендентних відносяться рівняння:
![]() ;
;
![]()
і інші подібні.
Розв’язання
трансцендентних рівнянь здійснюється звичайно на основі чисельних методів,
тобто шляхом спроб та помилок. Найбільш простий і очевидний метод розв’язання
такого рівняння – це випадковий пошук (або як його ще називають – метод
Монте-Карло). Він полягає у виборі випадкового значення ![]() та
підстановці його в рівняння, якщо
та
підстановці його в рівняння, якщо ![]() не підходить, то
вибирається наступне випадкове значення і т.д. Очевидно, що час, необхідний для
пошуку коренів рівняння методом Монте-Карло є досить великим і навіть при
застосуванні сучасної комп’ютерної техніки може бути неприйнятним.
не підходить, то
вибирається наступне випадкове значення і т.д. Очевидно, що час, необхідний для
пошуку коренів рівняння методом Монте-Карло є досить великим і навіть при
застосуванні сучасної комп’ютерної техніки може бути неприйнятним.
Існують також більш надійні методи, як наприклад, метод хорд чи метод ділення відрізка пополам. Розглянемо останній метод більш детально.
Для розв’язання трансцендентного рівняння спочатку слід його привести до стандартного вигляду:
![]()
Наприклад рівняння
![]()
в стандартному вигляді стане:
![]()
тобто
![]() .
.
Тепер розв’язання рівняння полягає в знаходженні
такого ![]() , для якого
, для якого
![]() ,
,
Де ![]() – максимально допустиме
значення абсолютної похибки (звичайно це значення залежить від задачі і
вибирається досить малим, наприклад
– максимально допустиме
значення абсолютної похибки (звичайно це значення залежить від задачі і
вибирається досить малим, наприклад ![]() ,
, ![]() і т.п.
і т.п.
Наступна задача полягає в визначенні інтервалу ізоляції, тобто такого проміжку, на якому обов’язково існує хоча б один корінь рівняння.
Звичайно інтервал
ізоляції визначається таким чином: якщо функція ![]() існує
на всьому проміжку
існує
на всьому проміжку ![]() , і
, і ![]() та
та ![]() мають різні знаки, то такий проміжок можна
вважати інтервалом ізоляції (так як графік функції обов’язково перетинає вісь
абсцис).
мають різні знаки, то такий проміжок можна
вважати інтервалом ізоляції (так як графік функції обов’язково перетинає вісь
абсцис).
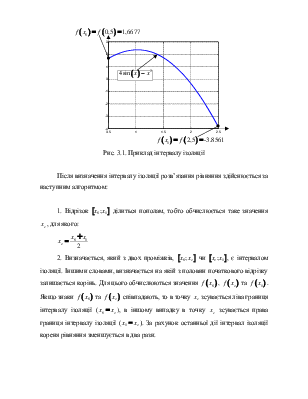
На рис. 3.1 показано приклад інтервалу ізоляції для рівняння
![]() .
.
Так як на
проміжку ![]() функція
функція ![]() не має
розривів, а значення функції
не має
розривів, а значення функції ![]() та
та ![]() мають різні знаки, то проміжок
мають різні знаки, то проміжок ![]() є інтервалом ізоляції.
є інтервалом ізоляції.
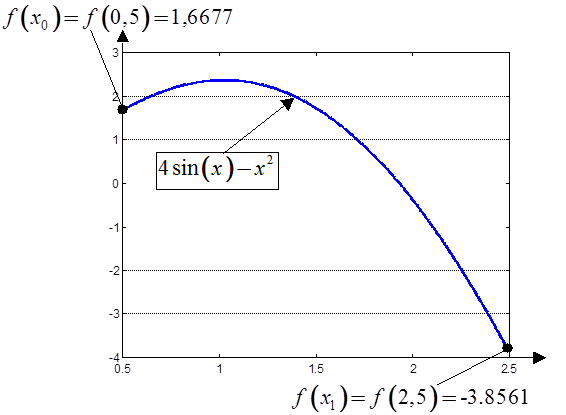
Рис. 3.1. Приклад інтервалу ізоляції
Після визначення інтервалу ізоляції розв’язання рівняння здійснюється за наступним алгоритмом:
1. Відрізок ![]() ділиться пополам, тобто обчислюється таке
значення
ділиться пополам, тобто обчислюється таке
значення ![]() , для якого:
, для якого:
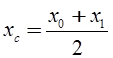
2. Визначається,
який з двох проміжків, ![]() чи
чи ![]() , є
інтервалом ізоляції. Іншими словами, визначається на якій з половин початкового
відрізку залишається корінь. Для цього обчислюються значення
, є
інтервалом ізоляції. Іншими словами, визначається на якій з половин початкового
відрізку залишається корінь. Для цього обчислюються значення ![]() ,
, ![]() та
та ![]() . Якщо
знаки
. Якщо
знаки ![]() та
та ![]() співпадають,
то в точку
співпадають,
то в точку ![]() зсувається ліва границя інтервалу ізоляції
(
зсувається ліва границя інтервалу ізоляції
(![]() ), в іншому випадку в точку
), в іншому випадку в точку ![]() зсувається права границя інтервалу
ізоляції (
зсувається права границя інтервалу
ізоляції (![]() ). За рахунок останньої дії інтервал
ізоляції кореня рівняння зменшується в два рази.
). За рахунок останньої дії інтервал
ізоляції кореня рівняння зменшується в два рази.
3. Перевіряється
умова досягнення необхідної точності розв’язання рівняння. Якщо ![]() то рівняння вважається розв’язаним, з
коренем, рівним
то рівняння вважається розв’язаним, з
коренем, рівним ![]() . В іншому випадку здійснюється
перехід на п. 1.
. В іншому випадку здійснюється
перехід на п. 1.
Напишіть програму, що працює за розробленим алгоритмом, та розв’яжіть за її допомогою рівняння
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.