Свойства детерминантов. Операции сложения и умножения матриц, страница 2

Пусть дана матрица  раз­меров иматрица  размеров . Матрицы таковы, что длина строки (т. е. число столбцов) первой равна   высоте столбца (числу строк) второй.  Возьмем строку с номером из матрицы  и столбец с номе­ром  из матрицы . Умножим каждый элемент вы­бранной строки на соответствующий элемент столбца и сложим полученные произведения, т.е. составим сумму

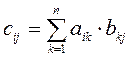
Мы выпишем такие суммы для всех и в виде матрицы размеров  (— номер строки, — номер столбца).

Определение. Матрицу , элементы которой вы­ражаются через элементы матриц  и  по формулам (3), назовем произведением  на и обозначим .

Умножение матриц не коммутативно. Даже если определены оба произведения  и , они могут быть не равны.

Если какие-нибудь матрицы  и  удовлетворяют соотношению , то они называются перестано­вочными. Перестановочные матрицы существуют.

На­пример, единичная матрица порядка  перестановочна с любой квадратной  матрицей того же порядка, т. е.

То обстоятельство, что каждая матрица  не ме­няется при умножении на единичную матрицу, пред­ставляет собой важное свойство единичной матрицы, которому она обязана своим названием.

Свойство 1. У множение матриц ассоциативно, т.е. если определены произведения  и , то определены   и выполнено равенство.

Доказательство: Пусть дана матрица  раз­меров ,матрица  размеров  и  размеров , то произведение имеет  размер , а произведение   будет размера . Элементы полученной матрицы

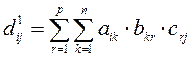
Поскольку  размеров  и  размеров , то определено  произведение  и размер полученной матрицы . Произведение   будет размера . Элементы полученной матрицы

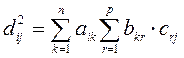
Поменяв местами суммы получаем

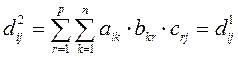
Что и требовалось доказать.

Свойство 2. Умножение матриц дистрибу­тивно по отношению к сложению

Доказательство: Пусть дана матрица  раз­меров ,тогда и матрица  должна иметь размер . Для того чтобы можно было умножать на матрицу  её размер должен быть , то произведение имеет  размер  и элементы этой матрицы будут

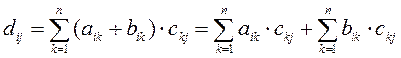
Первое слагаемое это элементы матрицы , а второе - , что и требовалось доказать.

Легко может быть доказано следующее свойство умножения матриц.

Свойство 3. Если произведение  имеет смысл, то

для любого числа .

Следующее свойство приведем без доказательства.

Свойство 4. Для любых квадратных матриц  и одного порядка

Проверим это свойство для определителей второго порядка.

  

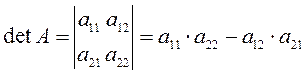
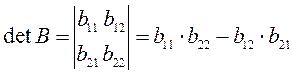
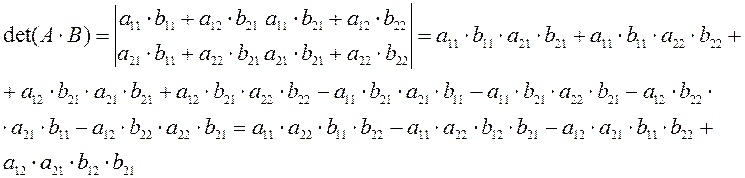
Что и требовалось доказать.

Свойство5. Если определено произведение , го определено и произведение  и выполнено равенство

Доказательство: Пусть матрицы  и  имеют соответственно размеры  и . По определению

Элементы матрицы  определяются по формуле

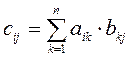
С учетом определения транспонированной матрицы, элементы матрицы  находятся по формуле

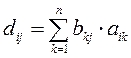
тогда видно, что . Утверждение доказано.

Пример. Найти  , если  A=.

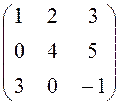Решение: Найдем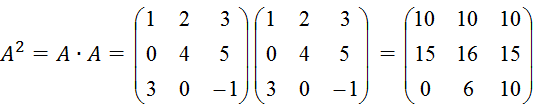

С учётом определения умножения матрицы на число, получаем

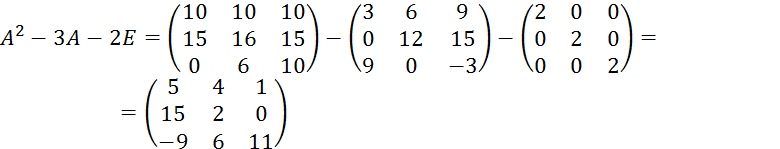
Обратная матрица. Исследуем теперь, насколько возможно ввести операцию деления, обратную операции умножения. Введем следующее определение.

Определение. Квадратная матрица , удовлетворяющая вместе с заданной матрицей равенствам

 (где  единичная матрица), назы­вается обратной к  

Из свойств умножения матриц имеем

Поэтому матрица может иметь обратную только тогда, когда ее детерминант не равен нулю.

Если у некоторой матрицы  существует обратная, то только одна.

Утверждение. У каждой квадратной матрицы  с детерминантом, не равным нулю, существует обратная матрица . Ее элементы находятся по формуле

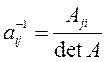
в которой через обозначено алгебраическое дополне­ние элемента  матрицы.

Доказательство: Найдем произведение

Элементы матрицы будут следующими

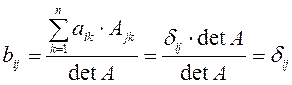
а это элементы единичной матрицы. Утверждение доказано.

Чтобы продемонстрировать удобство матричных обо­значений, рассмотрим еще раз правило Крамера. Си­стему из линейных уравнений с  неизвестными мы можем записать в виде

где  - квадратная матрица порядка , составленная из коэффициентов,  - столбец неизвестных,  - столбец свободных членов. Если матрица имеет обратную матрицу, то можно умножить слева обе части равенства на матрицу . Мы получим

учитывая, что 

получаем  

Этим показано, что решение единственно, если оно су­ществует, и найдено выражение этого решения через матрицу системы и столбец свободных членов.

Ранг матрицы

Число элементов в столбце мы будем называть его высотой, а число элементов в строке — ее длиной.

Два столбца называются равными, если они одной высоты и равны их элементы, имеющие одинаковые номера. Аналогично определяется равенство строк.

Определение. Суммой двух столбцов одной и той же высоты называется столбец, элементы которого равны суммам соответствующих элементов данных столбцов, т. е. по определению