Разработка схемы формирования вероятности безотказной работы и интенсивности потока отказов сложной технической системы

Моменты отказа элементов сложной системы при установив­шемся режиме работы [ма33]

Тогда по аналогии с формулой (2.5) интенсивность потока отказов машины, ее систем, узлов и деталей можно описать уравнениями:

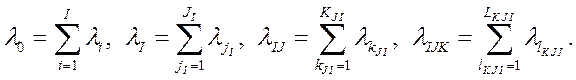                (2.9)

Отказы элементов сложной восстанавливающейся системы можно принять практически несвязанными друг с другом, тогда наработка между отказами является случайной величиной, рож­даемой процессом без последействия и распределенной по экспо­ненциальному закону [иг42]. Поэтому математическое ожидание наработки на отказ и интенсивность потока отказов связаны соответственно выражениями:

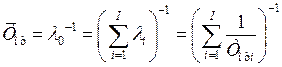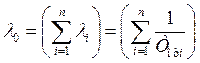,.                     (2.10)

Вероятность, что ремонтные работы не потребуются на промежутке времени  Т непрерывной эксплуатации

.                                                                 (2.11)

Коэффициент готовности машины при  условии, что учитываются только внезапные отказы [Гос27002], устраняемые посредством неплановых ремонтов:

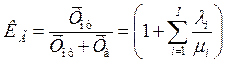,                                                            (2.12)

где - средняя наработка машины на отказ; - среднее время восстановления работоспособности (простоя в неплановом ремонте); µ_i - интенсивность потока восстановлений.

,                                                                       (2.13)

Т_вi – время восстановления работоспособности машины после отказа i-го элемента.

3.7. Оценка надежности машины как сложной восстанавливаемой системы с помощью теории массового обслуживания (ТМО)

Выражения для приведенных выше показателей выводились на основании интегральной характеристики – суммарного времени восстановления машины (за год) после внезапных отказов. ИАСУ способна анализировать информацию об отказах отдельных узлов. Используем  теорию массового обслуживания для описания вероятностей состояний машины на основании информации об интенсивностях потоков отказов λ_i(t) и восстановлений μ_i(t) отдельных из n-го количества узлов.

Выведем теоретическое выражение коэффициента готовности – комплексного показателя надежности технического объекта. Машина состоит из большого числа элементов, отказ кото­рых в процессе эксплуатации устраняют неплановым ремонтом. По­очередно в случайные моменты времени машина из исправно­го состояния (S₀) может переходить в состояние отказа первого элемента (S₁) или второго элемента и т.д. вплоть до S_n. Время простоя в неплановом ремонте также является случайной величи­ной, зависящей от характера повреждений элемента, наличия за­пасных частей и т.п. Если принять поток отказов и восстановле­ний простейшими, то машину можно рассматривать как систему массового обслуживания (СМО), показанную на рис. 3.37.

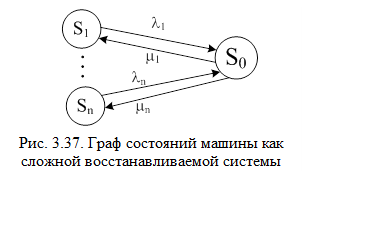Для установившегося режима граф СМО можно описать урав­нениями:

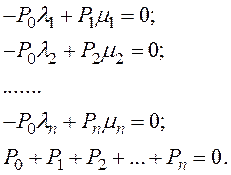
где р₀, р₁, р_n – вероятности нахождения системы соответственно в исправном состоянии (ноль отказов), с отказом первого элемента, с  отказом n-ного элемента; λ_1…n и μ_1…n – соответствующие интенсивности  потоков отказов и восстановлений.

Решая систему уравнений, можно выразить вероятности всех состояний в функции срока t службы:

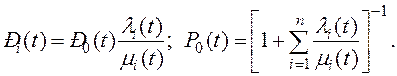                   (3.95)

Если учитывать только внезапные отказы, переводящие машину из работоспособного состояния в неработоспособное, то второе выражение будет соответствовать коэффициенту готовности.

Интенсивности потоков отказов и восстановлений элементов определя­ется величинами, обратными среднему времени соответственно наработки