Алгоритмы и методы интерполяции

Алгоритмы и методы интерполяции

Для работы УЧПУ существенное значение имеет алгоритм интерполяции. Под интерполяцией понимают выдачу информации о  траектории движений инструмента в интервале между координатами опорных точек, заданных в УП. Если траектория движения между опорными точками задана прямой, то выполняют линейную интерполяцию, если окружностью, то круговую интерполяцию.  Интерполяцию выполняют с помощью электронных схем ; (в УЧПУ Н22, НЗЗ и др.) либо с помощью ПМО (в микропроцессорных устройствах ЧПУ). Однако в обоих случаях интерполиру­ют по одним и тем же математическим выражениям. Интерполятор отрабатывает программу последовательно отдельными участками (кадрами), при линейной интерполяции— это участки прямых линий, расположенных в пространстве. Предположим, что необходимо отработать кадр, представляющий собой отрезок АВ При этом начало относительной системы коор­динат совпадает с началом отрабатываемого отрезка, т. е. координаты начала отрезка Хo'==0; Уo'==0, а координаты конца отрезка Х'к = X; У’к = У.

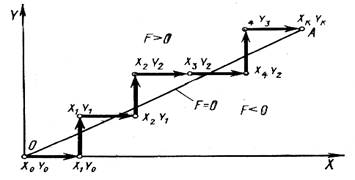
Рис. 3. Линейная интерполяция на участке ОА методом оценочной функции

Рассмотрим алгоритмы линейно-круговой интерполяции. Наибольшее распространение получил способ, опирающийся на решение дифференциальных уравнений прямой и окружности (метод цифровых дифференциальных анализаторов—ЦДА), и способ, в основу которого положено решение алгебраических уравнений (метод оценочной функции).

В большинстве УЧПУ линейно-круговая интерполяция производится по методу оценочной функции. Линейная интерполяция методом оценочной функции. Интерполируемая прямая ОА (рис. 3) разделяет плоскость XY на две области: F>0 (где значение оценочной функции F положительно) и F<.0 (где значение оценочной функции Fотрицательно). Область F>0 находится над прямой, область F<0 — ниже ее, интерполируемый отрезок ОА прямой представляет собой область, где F=0.

Если промежуточная точка траектории интерполяции (например, точка с координатами х1, у1) находится в области F > О, то следующий шаг (перемещение на одну дискрету) дается по оси X. Если же промежуточная точка траектории, например точка с координатами х2, y2, находится на области F < 0, то следующий шаг дается по оси У. Поскольку работа происходит в относительной системе коорди­нат, начало интерполируемого отрезка всегда находится в начале координат. При этом начальная точка траектории интерполяции находится в начале интерполируемого отрезка (в области F = 0) и имеет координаты Xо = 0; Yо = 0. Так как начальная точка траектории интерполяции находится в области F = 0, первый шаг делается по оси Х в точку с коорди­натами X1 = 1; Yо = 0- Эта точка находится в области F < 0, поэтому следующий шаг делается по оси У в точку с координатами X1 = l, у1 = 1. Эта точка находится в области F > 0 и следующий шаг делается по оси X. Шаги делаются непре­рывно (с частотой, определяемой блоком задания скорости) до тех пор, пока траектория интерполяции не достигнет конца отрез­ка с координатами Xk, Yk. Круговая интерполяция методом оценочной функции заключается в следующем. Окружность, на которой расположен интерполируемый отрезок дуги, разделяет плоскость XY на две области: F>0, лежащую вне круга, ограниченного окруж­ностью, и область F<0, лежащую внутри круга, ограниченного окружностью; са­ма окружность представляет собой область, где F=0 (см. рис. 4). Интерполируемый отрезок дуги имеет начальную точку с координатами Хо, Yо и конечную точку с координатами Xk, Yk(начало относительных координат находится в центре окружности),рис. 4.

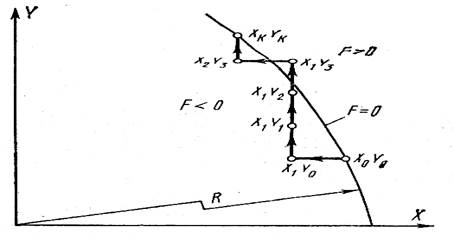
Рис. 4. Круговая интерполяция дуги ме­тодом оценочной функции с поочередными шагами по координатам Х и Y

Если промежуточная точка траектории интерполяции находится в области F > 0, то следующий шаг дается по оси X. Если же промежуточная точка траектории интерполяции находится в области F < 0, то следующий шаг дается по оси Y.