![]() - потери давления в сужающем устройстве с
номером
- потери давления в сужающем устройстве с
номером ![]() ;
;
![]() - длина цилиндрической части сужающего устройства
с номером
- длина цилиндрической части сужающего устройства
с номером ![]() ;
;
![]() - расход жидкости через поперечное сечение
трубопровода.
- расход жидкости через поперечное сечение
трубопровода.
Если допущения, использованные при выводе математической модели вискозиметра, выполняются в рабочих условиях, то с помощью этого вискозиметра можно определять вязкость различных жидкостей без индивидуальной калибровки на эталонных жидкостях. Однако математическая модель вискозиметра получена из уравнений ламинарного течения вязкой жидкости в стационарном режиме в предположении, что в сужающих устройствах трубопровода одинаковые потери давления, обусловленные затратами энергии на перестройку профилей скоростей при входе и выходе из цилиндрических частей этих сужающих устройств и другими факторами. При этом предполагается, что в поперечных сечениях цилиндрических частей сужающих устройств поддерживаются параболические профили скоростей. Но эти предположения выполняются приближенно даже в стационарных режимах течения вязких жидкостей. Другой недостаток этого вискозиметра связан с неизбежными отклонениями геометрической формы канала сужающего устройства от идеального кругового цилиндра. Этот фактор оказывает существенное влияние на результаты определения вязкости, так как диаметр канала входит в формулу (1) математической модели вискозиметра в четвертой степени. Однако до сих пор остаются нерешенными сложные проблемы прецизионного изготовления сужающих устройств и измерения их геометрических размеров (особенно измерения диаметра в разных поперечных сечениях по длине канала). Поэтому рассматриваемый вискозиметр не обеспечивает высокой точности измерения вязкости.
Сущность изобретения как технического решения, обеспечивающего измерение вязкости жидкостей в трубопроводах без индивидуальной калибровки на эталонных жидкостях и автоматическую компенсацию погрешностей определения вязкости, обусловленных неточностями используемой математической модели вискозиметра и погрешностями изготовления, выражается в совокупности следующих признаков:
- вискозиметр выполнен в виде системы автоматического обучения математической модели вискозиметра (ММВ) по величине сигнала рассогласования между измеренными значениями расхода и их оценками, вычисленными с помощью этой ММВ;
- система автоматического обучения ММВ образована термостатированным трубопроводом с двумя сужающими устройствами, расходомером, термометром, датчиками потерь давления в сужающих устройствах и цифровым вычислительным блоком, содержащим ММВ, генератор тестирующего шумоподобного сигнала, блок вычисления обучающих воздействий и оценок параметров ММВ, блок сравнения выходных сигналов расходомера и ММВ;
- априорная модель системы автоматического обучения ММВ образована нестационарным уравнением гидродинамики
![]() , (2)
, (2)
уравнением, описывающим зависимость вязкости от температуры:
![]() (3)
(3)
и уравнением расходомера
![]() ;
; ![]() , (4)
, (4)
где:
![]() - расход жидкости в момент времени
- расход жидкости в момент времени ![]() ;
;
![]() - кинематическая вязкость жидкости при
рабочей температуре
- кинематическая вязкость жидкости при
рабочей температуре ![]() ;
;
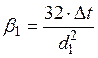 ;
; 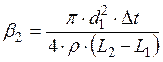 ;
; 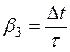 ;
;
![]() - потери давления в сужающем устройстве с
номером
- потери давления в сужающем устройстве с
номером ![]() , измеренные в момент времени
, измеренные в момент времени ![]() ;
;
![]() ,
,
![]() - параметры
ММВ (значения кинематической вязкости анализируемой жидкости при характерных
температурах
- параметры
ММВ (значения кинематической вязкости анализируемой жидкости при характерных
температурах ![]() и
и ![]() соответственно);
соответственно);
![]() - рабочая температура жидкости, измеренная в
момент времени
- рабочая температура жидкости, измеренная в
момент времени ![]() ;
;
![]() - плотность жидкости;
- плотность жидкости;
![]() - постоянная времени сглаживающего фильтра;
- постоянная времени сглаживающего фильтра;
![]() - выходной сигнал расходомера, измеренный в
момент времени
- выходной сигнал расходомера, измеренный в
момент времени ![]() ;
;
![]() - предел допустимой погрешности расходомера;
- предел допустимой погрешности расходомера;
![]() ,
,
![]() - ограниченные
по абсолютной величине обучающие воздействия на ММВ (относительные погрешности
ММВ, обусловленные погрешностями изготовления сужающих устройств, погрешностью
аппроксимации зависимости вязкости от температуры функцией
- ограниченные
по абсолютной величине обучающие воздействия на ММВ (относительные погрешности
ММВ, обусловленные погрешностями изготовления сужающих устройств, погрешностью
аппроксимации зависимости вязкости от температуры функцией ![]() и другими неконтролируемыми факторами);
и другими неконтролируемыми факторами);
![]() - относительная погрешность
измерения расхода, которая является ограниченным по абсолютной величине
возмущающим воздействием;
- относительная погрешность
измерения расхода, которая является ограниченным по абсолютной величине
возмущающим воздействием;
![]() ;
; ![]() ;
; ![]() ;
(5)
;
(5)
- обучающие воздействия ![]() ,
, ![]() и параметры ММВ
и параметры ММВ ![]() ,
, ![]() определяют
минимизацией регуляризованного функционала метода наименьших квадратов (МНК)
определяют
минимизацией регуляризованного функционала метода наименьших квадратов (МНК)
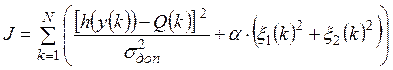 (6)
(6)
с параметром регуляризации ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.