Создание математической модели и алгоритма адаптивного управления гидроагрегата. Создание макета адаптивной системы управления гидроагрегата и проведение испытаний (Научное обоснование критериев оптимальности, принципов и методов, на базе которых Заявитель предлагает выполнять работу), страница 6

Показатель эффективности (8) предлагается использовать в системе управления активной мощностью для формирования задания ПИ-регулятору сервомотора механизма открытия НА. Алгоритм оптимального управления можно определить в результате решения задачи минимизации этого показателя с помощью принципа максимума.

3.2. Нормированное значение мощности турбины в установившемся режиме работы:

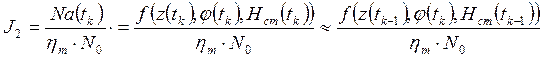,                      (9)

где:   - нормирующий множитель.

Показатель эффективности системы управления (9) определяет величину потерь мощности потока воды в турбине. Этот показатель предлагается использовать при разработке алгоритма коррекции комбинаторной зависимости:

угол разворота лопастей РК  в текущий момент времени  следует изменять так, чтобы показатель эффективности (9) принимал максимальное значение при любых (но известных) значениях статического напора и величины открытия НА  в момент времени .

Алгоритм решения этой задачи оптимального управления можно определить с помощью принципа максимума.

3.3. Квадрат среднеквадратической скорости штока сервомотора открытия НА:

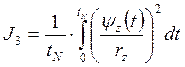.                                                                                          (10)

3.4. Квадрат среднеквадратической скорости штока сервомотора разворота лопастей РК:

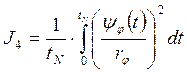.                                                                                        (11)

Показатели эффективности (10) и (11) определяют степень износа золотников и величину сил инерции. Эти показатели предлагается использовать при разработке алгоритмов управления сервомоторами открытия НА и разворота лопастей РК соответственно.

Таким образом, задача оптимального управления активной мощностью гидроагрегата заключается в определении оценок  и  переменных  и , обращающих в минимум показатели эффективности (8), (10), (11) и в максимум показатель эффективности (9). При этом следует учитывать ограничения, заданные:

·  дифференциальными уравнениями (5), (7) и (8);

·  неравенствами (6);

·  уравнениями, описывающими динамику ЭГП;

·  уравнениями, описывающими зависимость математического ожидания перепада давления от открытия НА и угла разворота лопастей РК;

·  уравнениями, описывающими зависимость активной мощности от открытия НА и угла разворота лопастей РК.

4. Обоснование математической модели объекта и алгоритма управления

4.1. Алгоритм оптимальной фильтрации турбулентных

пульсаций давления в расходомерном створе спиральной камеры

Алгоритм фильтрации турбулентных пульсаций давления предназначен для определения оптимальной оценки математического ожидания  перепада давления в зависимости от текущих значений статического напора, открытия НА и угла разворота лопастей РК.

Выходную переменную и параметры этой модели используют в алгоритме обучения модели процесса формирования активной мощности и в алгоритме формирования управляющих воздействий на ЭГП приводов лопаток НА и лопастей РК.

Математическое ожидание  перепада давления  в расходомерном створе спиральной камеры зависит от значений статического напора , открытия НА  и угла разворота лопастей РК  в текущий момент времени , где  – период опроса датчиков; . Эту неизвестную зависимость предлагается задать с помощью уравнений авторегрессии скользящего среднего (АРСС):

,                                                           (12)

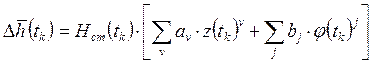,                                                       (13)

где:  - оценка выходного сигнала датчика перепада давления , вычисленная на момент времени  по уравнениям математической модели;  - турбулентные (случайные) пульсации давления.

Оптимальные оценки математического ожидания  перепада давления и параметров  и  формируют в процессе управления (в реальном масштабе времени) с помощью рекуррентного алгоритма оптимальной фильтрации турбулентных пульсаций  давления.

Этот алгоритм получают с помощью принципа максимума Понтрягина в форме рекуррентных уравнений расширенного фильтра Калмана для задачи оптимального оценивания переменной состояния и параметров  и  динамической системы (12), (13) минимизацией по переменным , ,  и  регуляризованного по Тихонову функционала метода наименьших квадратов: