Расчет перекрытия встроенного этажа корпуса, страница 2

Определим несущую способность сечений балок перекрытия, выполненных из стали марки ВСт3пс6. Расчет на прочность изгибаемых элементов выполняется по формуле

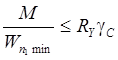
где М – изгибающий момент из статического расчета;

W_n,min – момент сопротивления сечения с учетом ослаблений отверстиями и др;

R_y – расчетное сопротивление стали. Для стали марки ВСт3пс6 R_y=235МПа;

g_с – коэффициент условий работы, для сечений прокатных сплошных балок, несущих статическую нагрузку g_с =1,1.

Несущая способность сечений определяется по формуле

Для двутавра №80Б2 W_x = 5760 см² :

М_п = 235 × 10³ ×1,1× 5760 × 10^-6 = 1489 кн×м.

 Для двутавра №60Ш1 W_x = 3680 см² :

М_п = 235 × 10³ ×1,1× 3680 × 10^-6 = 951 кн×м.

Для двутавра №40Б2 W_x = 928 см² :

М_п = 235 × 10³ ×1,1× 928 × 10^-6 = 240 кн×м.

Рассмотрим двухпролетную балку из двутавра №80Б2. Так как пролеты отличаются друг от друга не более чем на 10%, расчет ведем как для двухпролетной балки с равными пролетами. Принимаем L = 11.4 м.

Изгибающий момент на средней опоре от постоянной нагрузки будет:

Mв =(0,125 × 35,92+0,063  ) × 11,4² = 637,8 кн×м.

Несущая способность сечения 1489кн×м, следовательно временная нагрузкадолжна быть не более:

-  при нагрузке в обоих пролетах

(1489-637,8)/(0,125 × 11,4²) = 52,4 кн/м  или

при шаге балок 6 м  -  52,4 / 6 = 8,37 кн/м² (891 кгс/м²);

-  при нагрузке в одном из пролетов

(1489-637,8) / (0,063 × 11,4²) = 104 кн/м  или

104 / 6 = 17,3 кн/м² (1768 кгс/м²)

Изгибающий момент посередине пролета от постоянной нагрузки будет:

М₁ = (0,07 × 35,92+0,096 × 6,63) × 11,4² = 409 кн×м.

Временная нагрузка должна быть не более:

-  при нагрузке в обоих пролетах

(1489 – 409) / ( 0,125 × 11,4²) = 66,48 кн/м или

66,48 / 6 = 11,08 кн/м²  (1130кгс/м²)

-  при нагрузке в одном из пролетов

(1489 – 409) / (0,063 × 11,4²) = 132 кн/м  или

132 / 6 = 22 кн/м²  (2245 кгс/м²).

Рассмотрим однопролетную балку из двутавра №80Б2, например по осям 3/1, 4/1, 5/1, и 15/1. Пролет балок L=11,2 м.

Момент посредине  пролета от постоянной нагрузки равен

М=35,91 × 11,2² / 8 = 563 кн×м

Временная нагрузка должна быть не более

8 × (1489-563)/11,2² = 59 кН/м  или  59/6 = 9,8 кН/м² (1000кгс/м²)

Рассмотрим однопролетные балки пролетом 6 м из двутавра №60 Ш1 по осям 3/1, 4/1, 5/1.

Нормативная нагрузка от собственного веса конструкций составит

1,4 + 16 + 15 = 32,4 кН/м,

соответственно расчетная нагрузка –

1,4 × 1,05 + 16 × 1,1 + 15 × 1,1 = 1,47 + 17,6 + 16,5 = 35,57 кН/м.

Момент посредине пролета от постоянной нагрузки равен

М = 35,57 × 6² / 8 = 160 кН×м.

Несущая способность сечения М_и = 951 кН×м, тогда допускаемая временная нагрузка должна быть не более

8×(951-160) / 6² = 176 кН/м  или 176 / 6 = 29,3 кН/м²  (2990 кгс/м²).

Рассмотрим однопролетную балку из двутавта №40Б2 по оси 16/1 в осях В–Г.

 Наибольший момент от постоянной нагрузки

М = 28,01 × 6² / 8 = 126 кН×м.

Несущая способность сечения М_и = 240 кН×м, тогда допускаемая временная нагрузка должна быть не более

8×(240 – 160) / 6² = 25,3 кН/м  или 25,3 / 6 = 4,2 кН/м²  (430 кгс/м²)

2.3.4 Расчет жесткости балок

Определим допускаемою временную нагрузку на перекрытие встроенного этажа из условий жесткости стальных балок перекрытия. Стальные балки являются главными балками перекрытия, поэтому допускаемый прогиб должен быть не более 1/400 пролета. Для двухпролетной балки прогиб в середине одного из пролетов определяем методом Верещагина. Эпюры изгибающих моментов от постоянной нагрузки и эпюры от единичной силы приведены на рисунке   .

Перемножение эпюр:

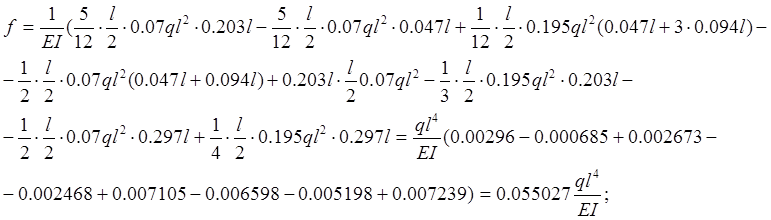Прогиб от постоянной нагрузки будет

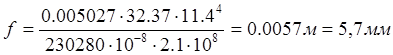
Определим теоретический прогиб от постоянной нагрузки с учетом веса перегородок. Эпюры изгибающих моментов от постоянной нагрузки и эпюры от единичной силы приведены на рисунке    .

 

Момент от нагрузки в пролете с перегородками обозначим через al²,в пролете без перегородок  cl². Момент на опоре через  bl², тогда

a = 0,07g + 0,096g^/ = 0,07 × 32,73 + 0,096 × 5,1 = 2,7807;

b = 0,125 × 32,73 + 0,063 × 501 = 4,4126;

c = 0,07 × 32,73 + 0,025 × 5,1 = 2,1636;

a + b = 2,7807 + 4,4126 = 7,1933; b + c = 4,4126 + 2,1636 = 6,5762.

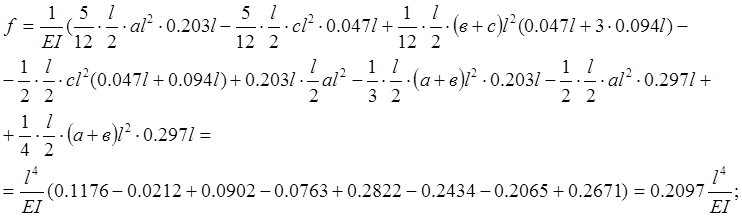
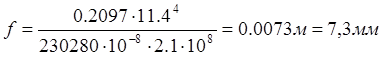
Допускаемый прогиб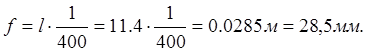

Наибольший прогиб от постоянной нагрузки составляет 25% допускаемого прогиба.

Проверим прогиб балок перекрытия пролетом 11,4м (балки по осям 3/1, 4/1, 5/1, и 15/1 в осях Б - В). Прогиб однопролетной балки с шарнирным опиранием по концам определяется по формуле

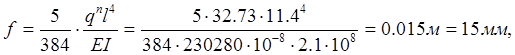
что составляет 53% от допускаемого прогиба.

Допускаемая временная нормативная нагрузка из условий жесткости составит (при шаге балок b = 6м):

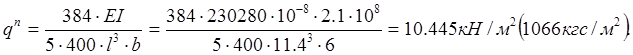
Определим прогиб наиболее нагруженной постоянной нагрузкой балки пролетом 6м (балка 40Б2 по оси 16/1 в осях В - Г):

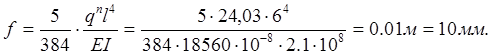
Допускаемый прогиб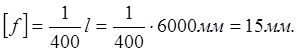

Прогиб от постоянной нагрузки составляет 67% допускаемого прогиба.

Допускаемая временная нормативная нагрузка из условий жесткости составит (при шаге балок b = 6м):

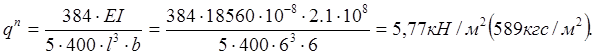
2.3.4  Проверка несущей способности плит перекрытия

В соответствии с серией 1.442.1 – 2, вып.1, плиты 2П1 – 3 при неагрессивной среде рассчитаны на нагрузку, с учетом собственного веса, равную 2525кгс/м² или 24,77кН/м².

Постоянная расчетная нагрузка с учетом собственного веса, приходящаяся на рядовую плиту перекрытия составляет (см. таблицу 3.3) 6,0кН/м². Следовательно, допускаемая временная расчетная нагрузка не должна превышать

p = 24,77 – 6,00 = 18,77кН/м² или 1915кгс/м².

Постоянная расчетная нагрузка с учетом собственного веса, приходящаяся на плиту перекрытия расположенную по оси В, в осях 13/1 – 14/1, составляет (см. таблицу 3.3) 11,41кН/м². Допускаемая временная расчетная нагрузка не должна превышать

p = 24,77 – 11,41 = 13,36кН/м² или 1363кгс/м².

Наибольшая расчетная нагрузка с учетом собственного веса плиты приходится на третью плиту перекрытия от оси А, в осях 15/1 – 16/1 и составляет (см. таблицу   ) 14,01кН/м². Допускаемая временная расчетная нагрузка не должна превышать

p = 24,77 – 14,01 = 10,76кН/м² или 1098кгс/м².