k - коэффициент, учитывающий изменение ветрового давления по высоте. Для типа местности В и высоты до 5 м, k5 = 0,5; при высоте от 5 до 10 м - k10 = 0,65 и от 10 до 20 м - k20 = 0,85.
Величина аэродинамического коэффициента для активного давления на вертикальную поверхность с наветренной стороны, Се = 0,8, для «отсоса» давление на вертикальную поверхность с заветренной стороны Се3 зависит от отношений h1/l b b/l, где l - ширина здания, b - длина, h1 - высота.
В нашем случае h1 / l = 12,6 / 24,6 = 0,51 > 0,5; b / l = 96 / 24,6 = 3,9 > 2.
Следовательно Се3 = - 0,51.
Величина коэффициента k для высоты h = 10,8 м и h = 12,6 м будут:
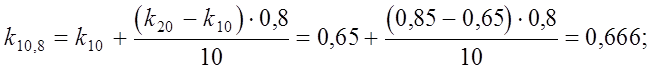
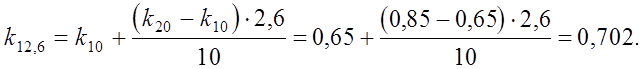
Тогда для ветровой нагрузки, действующей на парапет:
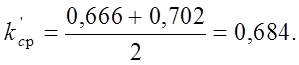
Активное давление на верх колонн от ветрового давления на парапет:
![]()
Отсос:
![]()
Величина коэффициента kср для ветровой нагрузки, действующей на высоте колонны:
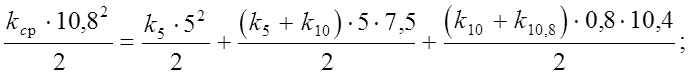
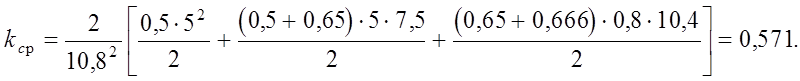
Распределенная нагрузка по высоте колонны (активное давление):
![]()
То же (отсос):
![]()
Расчетная схема рамы с действующими нагрузками приведена на рисунке
1.2.1 Определение усилий в сечениях колонн.
Закрепим рассчитываемую раму от смещений. В фиктивной связи под действием внешней нагрузки, приложенной к стойке, возникает реакция RB, величину которой определим с помощью таблицы 16.1 - 16.8 [ ].
Реакция RB распределяется между стойками рамы пропорционально их удельному сопротивлению сдвигу h, которое определяется по формулам:
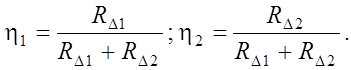
где RD1 и RD2 - горизонтальные реакции в опорах стоек от взаимного смещения концов стоек на единицу, определяемые по таблице 16.9 [ ].
Очевидно h1 + h2 = 1.
Моменты инерции поперечных сечений колонн по осям «А» и «Д» равны:
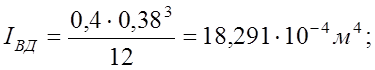
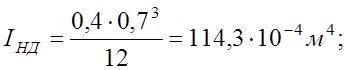
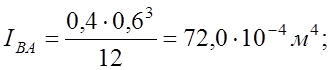
![]()
Отношения моментов инерции и длин верхней и нижней частей стоек следующие:
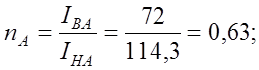
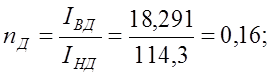
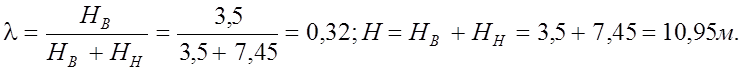
Реакция RD вызываемая горизонтальным смещением D = 1:
для стойки по оси «Д»:
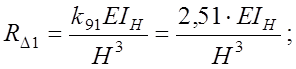
для стойки по оси «А»:
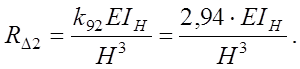
Тогда 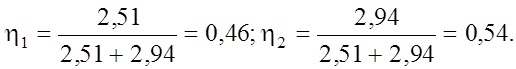
Поперечную раму рассчитываем на следующие виды загружения: 1 - постоянную нагрузку; 2 - снеговую нагрузку; 3 - ветровую нагрузку, действующую слева-направо и 4 - ветровую нагрузку, действующую справа-налево.
Колонны по оси «А» в осях «1-5» дополнительно проверяем на действие крановой нагрузки от кран-балки грузоподъемностью 5,0 тс.
Стойка по оси «Д».
Смещение геометрических осей сечений подкрановой и надкрановой частей стойки: е = (0,7 - 0,38) / 2 = 0,16 м.
Загружение 2, рисунок .
Величина снеговой нагрузки на покрытии пролета Ns = 71 кН.
По таблице 16.1, для n = 0,16; l = 0,32 и yв = 0 по интерполяции находим:
![]()
Величина горизонтальной реакции RBS равна:
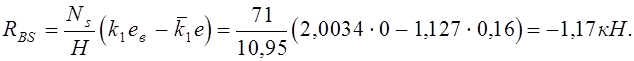
Усилия в сечениях стойки:
изгибающие моменты:
![]()
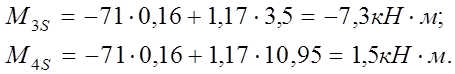
продольные силы
N1 = N2 = N3 = N4 = 71 кН.
Загружение 1, рисунок .
Постоянная нагрузка. Усилия в стойке от силы Ng получаем умножением усилий от Ns (загружение 2) на коэффициент:
k1,2 = Ng / Ns = 246 / 71 = 3,465.
![]()
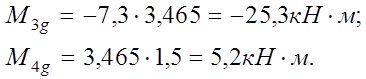
Для определения усилий в стойке от собственного веса стен находим величину горизонтальной реакции RВ:
1) по таблице 16.1 для sвп = 59,4 кН, евп = 0,25 м, при n = 0,16; l = 0,32; yв = 0,34 Нв:
![]()
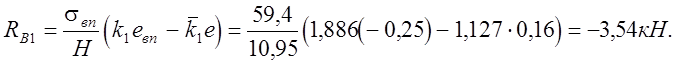
2) по таблице 16.2 для sсп = 98,2 кН, есп = 0,41 м, при n = 0,16; l = 0,32; y = 3,75м = 0,5 Нн:
![]()
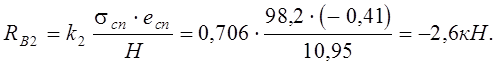
Суммарный момент от всей постоянной нагрузки будет:
![]()
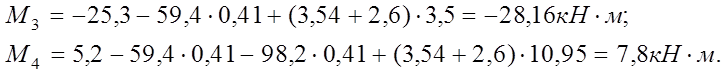
Моментом от собственного веса надкрановой части колонны пренебрегаем.
Продольные усилия:
N1 = 246 кН; N2 = 246 + 59,4 + 14,6 = 320 кН;
N3 = N2 = 320 кН; N4 = 320 + 98,2 + 57,4 = 475,6 кН.
Загружение 3. Ветровая нагрузка слева-направо.
Определим реакции RВ в стойках. По таблице 16.7 для стойки по оси «А» при n = 0,63; l = 0,32 по интерполяции находим k7 = 0,37, тогда:
RВ(А) = k7 wa H = 0,37 ´ 0,883 ´ 10,95 = 3,58 кН.
Для стойки по оси «Д» при n = 0,16; l = 0,32 по интерполяции находим k7 = 0,333, тогда: RВ(Д) = k7 w0 H = 0,333 ´ 0,563 ´ 10,95 = 2,05 кН.
Усилие в дополнительной связи:
![]()
Распределяем усилие в дополнительной связи между стойками:
![]()
![]()
Определяем усилия в расчетных сечениях стоек. Стойка по оси «А»:
![]()
![]()
Стойка по оси «Д»:
![]()
![]()
Загружение 4. Ветровая нагрузка справа-налево.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.