Объединение граф-схем алгоритмов, страница 9

Подграф ОГСА, соответствующий табл. 26.8 показан на рис. 26.2. Система формул перехода для этой подматрицы ; ; .

При построении рис. 26.2 выполнено совмещение с наложением трех операторов  в один.

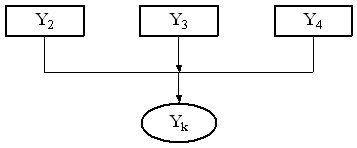
Рисунок 26.2 – Подграф ОГСА, соответствующий подматрице

В соответствии с табл. 26.7 выполняем следующую систему формул перехода

Формулы перехода различных подматриц между собой не связаны, а внутри одной и той же системы (подматрицы) их следует представить в минимальной форме так, чтобы между формулами перехода одной системы было как можно больше общих частей. Выгодна ситуация, когда некоторые формулы перехода целиком входят в другую более сложную формулу перехода (ФП). Например, выгодно если  войдет в .

С целью нахождения минимальной скобочной формы представления для  используем метод графов (рис. 26.3)

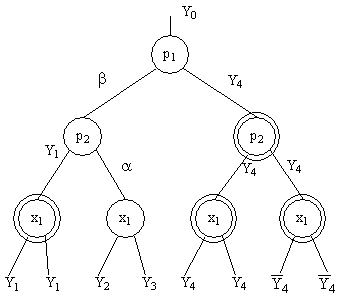
Рисунок 26.3 – Граф, представляющий формулу перехода

Левая дуга (ребро), выходящее из вершины ; соответствует ; соответственно, правая – ;. Концевые ребра отмечены входящими операторами или неопределенны (черточки). Вершины с одинаковыми входными отметками называются сходными (обведены двойным кругом). Чем больше в графе сходных вершин и чем они выше расположены, тем проще будет минимальная СКФ. Число условных вершин в подграфе ГСА равно числу несходных вершин в графе формулы перехода. Два правых ребра, так как они неопределенны, для увеличения сходности отметим операторами  и .