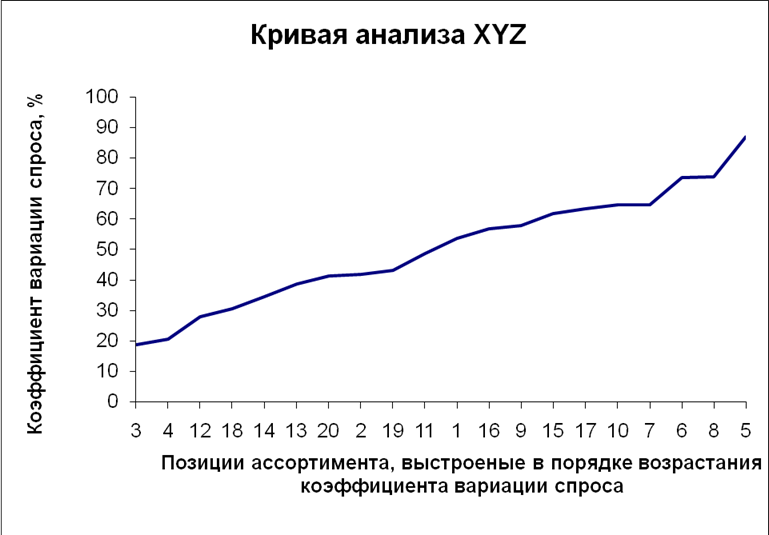
Таблица № 3 – Распределение позиций
|
AX |
AY |
AZ 6,12,2,11 |
|
BX |
BY |
BZ 14,18,4,19,16,17 |
|
CX |
CY 15 |
CZ 3,1,9,10,7,8,5,20,15,13 |
Вывод: Для позиции 6,12,2,11 вырабатывается индивидуальная схема управления запасами, и они требуют максимальных финансовых вложений; позиции 15 требуют ежедневного контроля; позиции 14,18,4,19,16,17 – управление этими запасами осуществляется как по индивидуальной, так и по общей схеме; позиции 3,1,9,10,7,8,5,20,15,13– планирование системы этих запасов осуществляется на длительный срок с ежедневной проверкой товара на складе.
Задача № 2
Логистика запасов
Задача 2.1 Определение оптимального уровня заказа
Исходные данные:
![]() =110
руб;
=110
руб; ![]() =50
руб;
=50
руб; ![]() =710
шт;
=710
шт; ![]() =0,6;
=0,6;
![]() =0,3;
=0,3;
![]() =0,7;
=0,7; ![]() =0,3;
=0,3;
![]() =0,91;
=0,91;
![]() =0,09.
=0,09.
Для определения оптимальной величины заказа используем формулу:
![]() ,
,
где ![]() – оптимальная величина заказа;
– оптимальная величина заказа; ![]() – затраты связанные с выполнением
одного заказа;
– затраты связанные с выполнением
одного заказа; ![]() – потребление данной партии;
– потребление данной партии; ![]() – коэффициент (0…1);
– коэффициент (0…1); ![]() – цена единицы продукции;
– цена единицы продукции; ![]() – доля от цены продукции
приходящаяся на затраты по хранению.
– доля от цены продукции
приходящаяся на затраты по хранению.
![]() ;
;
Необходимо выполнить итерацию:
![]()
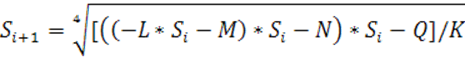 ,
,
где ![]() – расчетные коэффициенты:
– расчетные коэффициенты:
![]() = 0,11;
= 0,11;
![]() = 2,27;
= 2,27;
![]() = - 270,67;
= - 270,67;
![]() = - 5814,9;
= - 5814,9;
![]() = - 29397,55.
= - 29397,55.
![]() – это коэффициенты, отражающие
предварительное снижение стоимости продукции;
– это коэффициенты, отражающие
предварительное снижение стоимости продукции;
![]() – это коэффициенты, отражающие
скачки скидок.
– это коэффициенты, отражающие
скачки скидок.
![]() = 48,09.
= 48,09.
Проверим условие:
48.09 - 42,24 = 5,85
5,85 > 1 условие не выполняется, поэтому
рассчитываем ![]() :
:
![]() = 49,91.
= 49,91.
Проверим условие:
49,91 - 48,09 = 1,82
1,82 > 1 условие не выполняется, поэтому
рассчитываем ![]() :
:
![]() = 50,43.
= 50,43.
50,43-49,91=0,52
0,52 < 1 условие выполняется.
Вывод: Оптимальной величиной заказа будет S2 = 49,91.
Задача 2.1 Определение оптимального уровня заказа
Исходные данные:
![]() = 4000 т/год;
= 4000 т/год; ![]() = 16 у.д.е. за 1 п;
= 16 у.д.е. за 1 п; ![]() = 4 у.д.е. за 1 т.
= 4 у.д.е. за 1 т.
Необходимо определить оптимальный размер заказа с учётом затрат на хранение и транспортировку.
Величина суммарных затрат:
![]() ;
;
![]() ,
,
где ![]() – количество партий доступных за
расчетный период;
– количество партий доступных за
расчетный период; ![]() – тариф на транспортировку одной
партии;
– тариф на транспортировку одной
партии; ![]() - затраты на хранение запасов.
- затраты на хранение запасов.
![]() ,
,
где ![]() – объём потребления;
– объём потребления; ![]() – размер одной партии заказа.
– размер одной партии заказа.
![]() ,
,
где ![]() – расходы связанные с хранением.
– расходы связанные с хранением.
Выведем формулу величины суммарных затрат:
![]() .
.
![]() ,
,
![]() шт,
шт,
![]() руб,
руб,
![]() руб,
руб,
![]() = 716 руб.
= 716 руб.
|
|
100 |
150 |
179 |
200 |
250 |
|
|
200 |
300 |
358 |
400 |
500 |
|
|
640 |
427 |
358 |
320 |
256 |
|
|
840 |
727 |
716 |
720 |
756 |
Составим график:
Вывод: Из графика видно, что оптимальный размер заказа равен 179 шт.
Задача № 3
Система управления запасами
Система с фиксированным размером заказа
Исходные данные:
1) Потребность: 1650 шт;
2) Оптимальный размер заказа: 95 шт;
3) Время поставки: 8 дней;
4) Возможная задержка в поставке: 1 день;
5) Ожидаемое дневное потребление: 7 шт/день;
6) Срок расхода заказа: 14 дней;
7) Ожидаемое потребление за время поставки: 56 шт;
8) Максимальное потребление за время поставки: 63шт;
9) Гарантийный запас: 7 шт;
10) Пороговый уровень запаса: 63 шт;
11) Максимальный желательный запас: 102 шт;
12) Срок расхода МЖЗ: 6 дней.
Задача 3.1 График поведения системы без сбоев в поставке
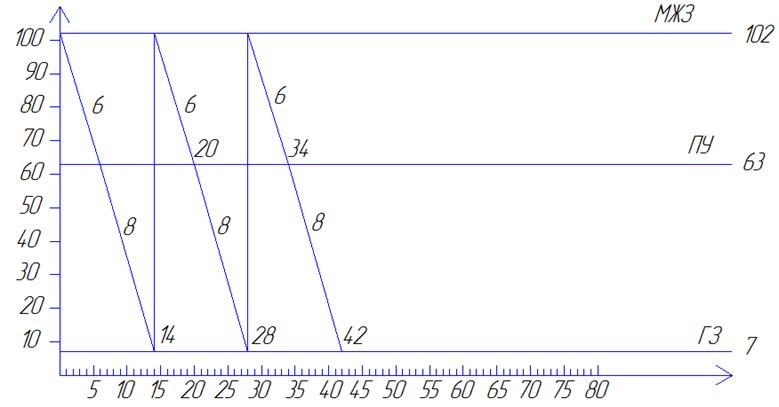
Задача 3.2 График поведения системы с единичным сбоем в поставке
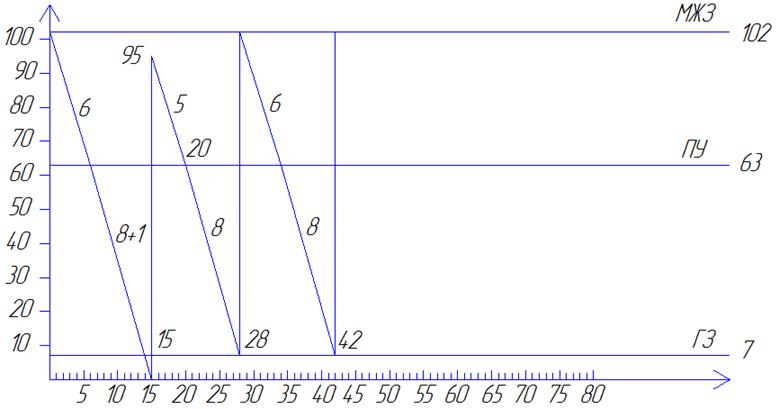
Задача 3.3 График поведения системы с систематическими сбоями в поставке
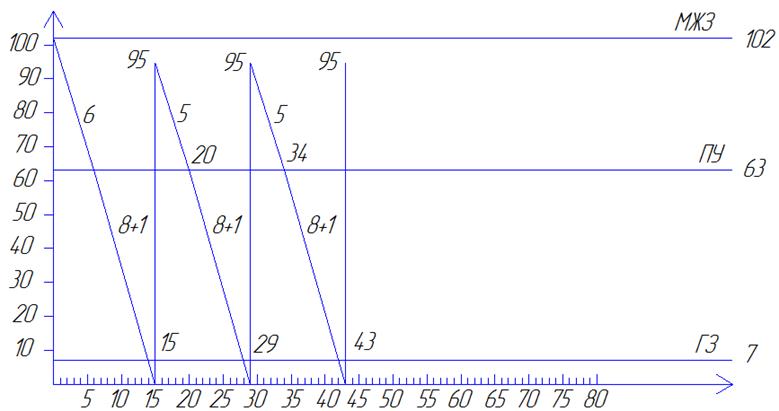
Система с фиксированным интервалом времени между заказами
Исходные данные:
1) Потребность: 1750 шт;
2) Оптимальный размер заказа: 90 шт;
Интервал времени между заказами: 13 дней;
3) Время поставки: 6 дней;
4) Возможная задержка в поставке: 1 день;
5) Ожидаемое дневное потребление: 7 шт/день;
6) Срок расхода заказа: - дней;
7) Ожидаемое потребление за время поставки: 42 шт;
8) Максимальное потребление за время поставки: 49шт;
9) Гарантийный запас: 7 шт;
10) Пороговый уровень запаса: 49 шт;
11) Максимальный желательный запас: 98 шт;
12) Срок расхода МЖЗ: 7 дней;
13) Размер поставки: 91 шт.
Задача 3.4 График поведения системы без сбоев в поставке
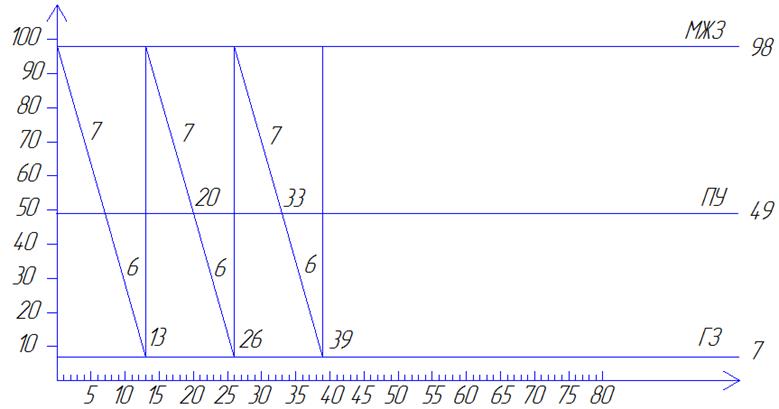
Задача 3.5 График поведения системы с единичным сбоем в поставке
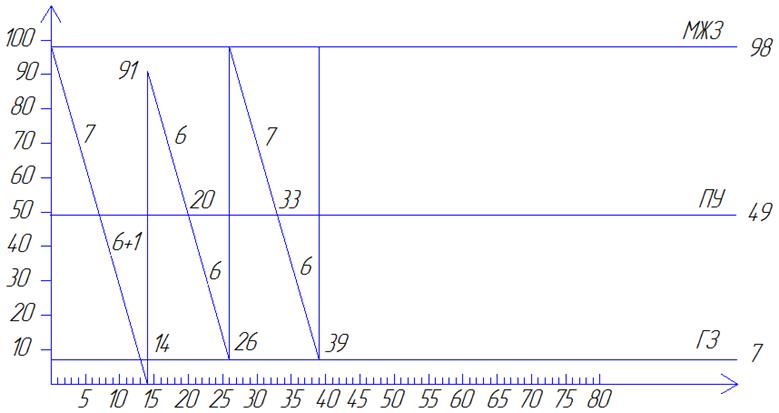
Задача 3.6 График поведения системы с систематическими сбоями в поставке
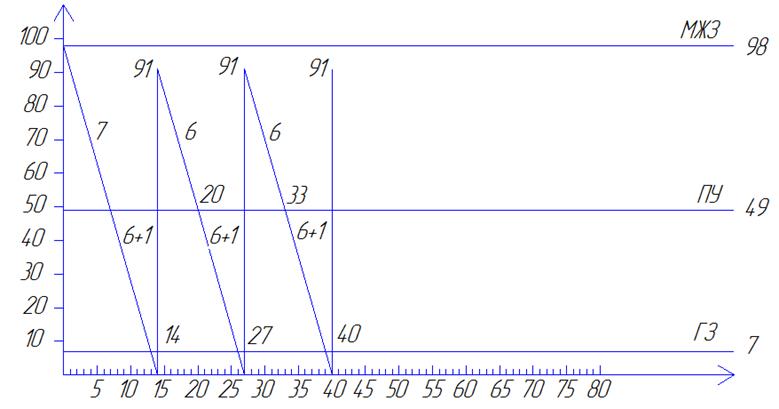
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.