Теоретическая механика: Банк заданий аттестационно-педагогических измерительных материалов (дидактическая единица ГОС - Кинематика точки. Кинематика твердого тела), страница 9

В планетарном механизме с внутренним зацеплением зубчатое колесо 1, катящееся по внутренней поверхности неподвижного колеса 2, приводится в движение кривошипом ОА, вращающимся вокруг неподвижной оси O с постоянной угловой скоростью .

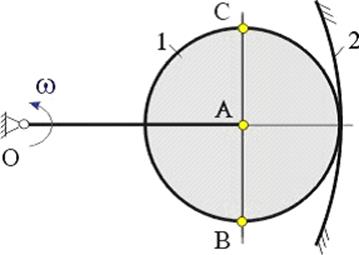
Мгновенный центр колеса 1 находится …

!TRUE

находится на прямой, содержащей отрезок ОА, левее точки A

!FALSE

находится на прямой, содержащей отрезок BC, выше точки A

!FALSE

находится  на прямой, содержащей отрезок BC, ниже точки A

!FALSE

находится на прямой, содержащей отрезок ОА, правее точки A

!FALSE

не существует

!TASK 1

Плоская фигура не поступательно движется по неподвижной плоскости, точка Q — это мгновенный центр ускорений фигуры.

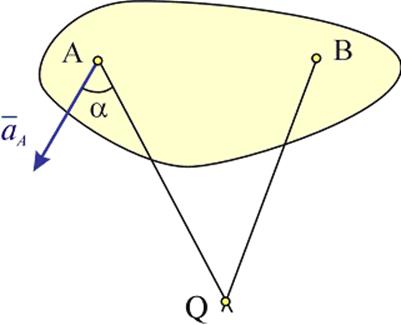
Ускорение точки B …

!TRUE

отклоняется от отрезка BQ на угол  в направлении хода стрелки часов

!FALSE

направлено вдоль отрезка BQ от точки B к точке Q

!FALSE

направлено перпендикулярно к отрезку BQ вправо

!FALSE

отклоняется от отрезка BQ на угол  в направлении, противоположном ходу стрелки часов

!FALSE

направлено перпендикулярно к отрезку BQ влево

!TASK 2

Ускорения точек A и B плоской фигуры параллельны, причем .

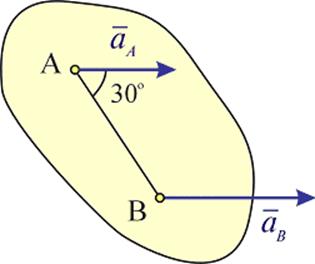
Вектор ускорения точки A будет направлен к МЦУ фигуры, если его повернуть вокруг точки A на угол …

!TRUE

 против часовой стрелки

!FALSE

 против часовой стрелки

!FALSE

 по часовой стрелке

!FALSE

 по часовой стрелке

!FALSE

 по часовой стрелке

!TASK 3

Ускорения точек A и B плоской фигуры параллельны, причем .

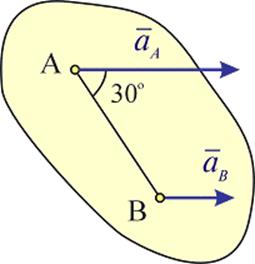
Вектор ускорения точки A будет направлен к МЦУ фигуры, если его повернуть вокруг точки A на угол …

!TRUE

 по часовой стрелке

!FALSE

 против часовой стрелки

!FALSE

 против часовой стрелки

!FALSE

 по часовой стрелке

!FALSE

 по часовой стрелке

!TASK 4

Квадрат АВСD движется в своей плоскости так, что в данный момент ускорения точек A и C направлены, как указано на рисунке, причем .

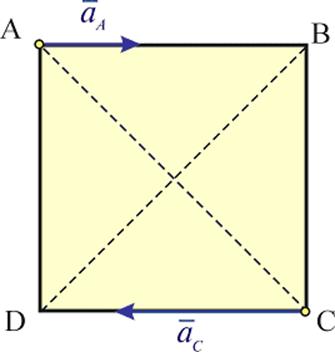
Мгновенный центр ускорений квадрата находится …

!TRUE

на диагонали АС ближе к точке A

!FALSE

на стороне AB

!FALSE

на стороне ВС

!FALSE

на диагонали ВD

!FALSE

в точке пересечения диагоналей АС и ВD

!END

!TASKFILE теормех 2.02.07# Полное ускорение точки при координатном задании движения

!DE= теормех-1-2#Кинематика точки

!TYPE=6

!TIME=2

Спецификация банка заданий АПИМ

1. Составители: Латышев В.И., Булатов Л.А., Митяев А.Г.

2. Дисциплина: Теоретическая механика

3. Объем часов: группа 1

4. Дидактическая единица ГОС: Кинематика точки

5. Тема задания: Полное ускорение точки при координатном задании движения

6. Уровень сложности – 2 (знать и уметь)

7. Ориентировочное время выполнения задания – 2 минуты

8. Перечень контролируемых учебных элементов

Студент должен знать: координатныйспособ задания движения точки

уметь: определять полное ускорение точки

9. Дата создания - сентябрь 2007

10. Количество заданий в данном файле – 5

!TASK 0

Точка движется согласно уравнениям  ( — в метрах). Модуль ускорения точки (в ) равен …

!TRUE

!TASK 1

Точка движется согласно уравнениям  ( — в метрах). Модуль ускорения точки (в ) равен …

!TRUE

!TASK 2

Точка движется согласно уравнениям  ( — в метрах). Модуль ускорения точки (в ) равен …

!TRUE

!TASK 3

Точка движется согласно уравнениям  ( — в метрах). Модуль ускорения точки (в ) равен …

!TRUE

!TASK 4

Точка движется согласно уравнениям  ( — в метрах). Модуль ускорения точки (в ) равен …

!TRUE

!End

!TASKFILE теормех 2-2-01# Скорость при координатном способе задания движения

!DE= теормех-1-2#Кинематика точки

!TYPE=6

!TIME=2

Спецификация банка заданий АПИМ

1. Составители: Латышев В.И., Булатов Л.А., Митяев А.Г.

2. Дисциплина: Теоретическая механика

3. Объем часов: группа 1

4. Дидактическая единица ГОС: Кинематика точки

5. Тема задания: Скорость при координатном способе задания движения

6. Уровень сложности – 2 (знать и уметь)

7. Ориентировочное время выполнения задания – 2 минуты

8. Перечень контролируемых учебных элементов

Студент должен знать: способы задания движения точки

уметь: определять  и направлять вектор скорости точки

9. Дата создания - сентябрь 2007

10. Количество заданий в данном файле – 5

!TASK 0