Предложены Хопкрофтом в 1973 г.
В 2-3 дереве
1) Каждый внутренний узел имеет 2 или 3 сына.
2) Все пути от корня до любого листа имеют одинаковую длину.
3) Элементы располагаются в листьях 2-3 дерева.
4) В каждый внутренний узел записывается ключ наименьшего элемента, являющегося потомком второго сына и ключ наименьшего элемента, - потомка третьего сына, если третий сын есть.
 |
7 16
 |
|
|
5 - 8 12 19 -
2 5 7 8 12 16 19
k-1 k-1
2-3 дерево с k уровнями имеет от 2 до 3 листьев, то есть 2-3 дерево, содержащее n элементов, имеет высоту не менее 1+log3 n и не более 1+log2 n. Таким образом высота дерева имеет порядок О(log n).
Элемент можно найти за время О(log n), сравнивая ключ искомого элемента с параметрами в узлах.
Если ключ меньше, чем минимальный элемент у второго сына, то выбирается первый сын. Иначе, если узел имеет двух сыновей, выбирается второй сын. Если есть третий сын, то выбирается второй сын, если ключ меньше минимального ключа третьего сына, или третий сын в противном случае. Таким образом поиск приводит к листу с искомым ключом.
Включение нового элемента начинается так же, как и процесс поиска. Пусть мы находимся в некотором внутреннем узле x, чьи сыновья – листья и не содержат элемента с заданным ключом k. Если узел содержит двух сыновей, то новый элемент подключается к этому узлу в качестве третьего сына. Новый элемент помещается так, чтобы не нарушить упорядоченность сыновей. После этого корректируются значения минимальных ключей в узле x.
Например, включаем элемент с ключом 18.
При поиске мы приходим к самому правому узлу на среднем уровне. Помещаем 18 среди сыновей этого узла в порядке 16, 18, 19. В узле записываются значения 18 и 19.
7 16
 |
5 8 12 18 19
 |
|
|
|
|
|
|
|
2 5 7 8 12 16 18 19
Если при подключении к узлу новый элемент является четвертым, то узел x разбивается на 2 узла x и x’. Два наименьших элемента переносятся в узел x, а два наибольших – в x’. Теперь надо вставить узел x’ среди сыновей родителя узла x. Здесь ситуация повторяется. Если родитель имеет двух сыновей, то узел x’ становится третьим сыном. Если родитель имеет трех сыновей, то он в свою очередь разбивается на два узла. Процесс идет в случае необходимости выше и может достигнуть корня дерева. При необходимости разбиения корня создается новый корень, сыновьями которого становятся два узла, получившиеся при разбиении старого корня.
Пусть мы вставляем элемент m с ключом 10. Выбранный узел до подключения имеет трех сыновей, поэтому он разбивается на два новых узла.
|
7 16
 |
|
|
|
5 - 8 - 12
- 18 19
 |
|
|
|
|
|
|
|
|
2 5 7 8 10 12 16 18 19
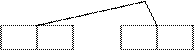
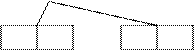
Корень разбивается на два узла и создается новый корень.
 |
10 -
7
- 16
 |
 |
5 - 8
- 12 - 18 19
2 5 7
8 10 12 16 18 19
struct Internal { type=INTERNAL
T low2, low3
Internal son1, son2, son3
};
struct Leaf { type=LEAF
T key
T1 data
};
T23_Insert(t,x)
1
x – элемент данных
2
t – корень 2-3 дерева
3
lt new Leaf(x)
4 if t=nil
5
then t new Internal
6
son1[t] lt
7 son2[t] son3[t]
nil
8 return t
9 if son2[t]=nil
10
then son2[t] lt
11 low2[t] key[lt]
12 return t
13 Insert1(t,lt,tbk,lbk)
14
if tbk=nil
15
then temp t
16
t new Internal
17
son1[t] temp
18
son2[t] tbk
19
low2[t] lbk
20
son3[t]
nil
21 return t
Первоначально дерево пусто и указатель на корень дерева root=nil.
Вызов функции:
Root
T23_Insert(root,x)
T23_Insert1(&t,<,&tnew,&low)
1 t – корень 2-3 дерева/2-3 поддерева
2 lt – новый узел - лист
3
tnew – адрес нового узла, передаваемого
родителю
4
low – минимальный ключ в поддереве нового
узла tnew
5
tnew nil
6
t - лист
7 if t - лист
8
then if key[t]=key[lt]
9
then tnew t или lt с
большим ключом
10
low больший из key[t]
и key[lt]
11 return
12
t – внутренний узел
13 выбрать w – сына t узла для вставки lt
14 T23_Insert1(w,lt,tbk,lbk)
15
if tbk=nil
16 then вставка tbk среди сыновей узла t, справа от w
17 if t имеет 4 сына
18 then создание нового внутреннего узла tnew
19 перенос двух правых сыновей узла t в узел tnew
20
low минимальный ключ первого сына tnew
21 return
Более подробный псевдокод операции вставки в 2-3 дерево приведен ниже.
T23_Insert1(&t,<,&tnew,&low)
1 t – корень 2-3 дерева/2-3 поддерева
2 lt – новый узел - лист
3
tnew nil
4 if type[t]=LEAF
5
then if key[t]=key[lt]
6
then tnew lt
7 if key[t]<key[lt]
8
then low key[lt]
9
else low key[t]
10
temp t
11
t lt
12
lt t
13 return
14
t – внутренний узел
15 if key[lt]<low2[t]
16
then child 1
17
w son1[t]
18 else if son3[t]=nil or key[lt]<low3[t]
19
then child 2
20
w son2[t]
21
else child 3
22
w son3[t]
23 T23_Insert1(w,lt,tbk,lbk)
24
if tbk=nil
25
вставка нового сына
26 then if son3[t]=nil
27
then узел имел 2-х
сыновей
28
if child=2 вставка во второе поддерево
29
then son3[t] tbk
30
low3[t] lbk
31 else вставка в первое поддерево
32
son3[t]
son2[t]
33
low3[t] low2[t]
34
son2[t] tbk
35
low2[t]
lbk
36
else узел имел 3-х сыновей
37
tnew new Internal
38 if child=3
39
then вставка в третье поддерево
40
son1[tnew] son3[t]
41
son2[tnew] tbk
42
son3[tnew] nil
43
low2[tnew] lbk
44
son3[t] nil
45
low low3[t]
46 else child<=2
47
son2[tnew] son3[t]
48
low2[tnew] low3[t]
49
son3[tnew] nil
50
son3[t] nil
51 if child=2
52
then son1[tnew] tbk
53
low lbk
54 if child=1
55
then son1[tnew] son2[t]
56
son2[t] tbk
57
low low2[t]
58
low2[t] lbk
59
конец then 26
60 return
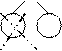
Если при удалении узла x-листа, у родителя w остается один сын и узел w является корнем, то родитель удаляется из дерева, а корнем становится его единственный сын. Пусть родитель w не является корнем. Тогда, если братья узла-родителя w имеют трех сыновей, то один из сыновей брата передается узлу w и у него становится двое сыновей. Если братья узла w имеют двух сыновей, то единственный сын узла w передается одному из его братьев, и узел w удаляется. Если после этого у родителя удаленного узла w останется один сын, то процесс перестройки повторяется дальше по дереву.
 |
|
10 - 12 -
7 - 16 - 7
- 18 -
5 - 8 - 12
- 18 - 5 - 8 - 16
- 19 -
 |
 |
 |
 |
 |
|
 |
|
|
|
|
|||||||||||
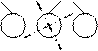2 5
7 8 10 12 16 18 19 2 5 7 8
12 16 18 19
 |
|
 |
|||
12 - 12 -
 |
 |
 |
7 - 18
- 12 18
|
|
|
|
|
|
5 8 16 - 19 - 5
8 16 - 19 -
2 5 8 12 16 18 19 2 5
8 12 16 18 19
12 18
 |
|||
 |
|||
5 8 16 - 19 -
 |
 |
 |
 |
2 5 8 12 16 18 19
Рекурсивная операция T23_Delete(t,x) по заданному указателю на удаляемый узел x отыскивает узел x в 2-3 дереве и удаляет его. Если после удаления родитель узла x имеет одного сына, то функция возвращает значение TRUE, иначе – FALSE.
T23_Delete1(t,x)
1
t – узел корня 2-3 дерева/2-3 поддерева
2
x – удаляемый узел-лист
3 if сыновья t - листья
4 then if x принадлежит к сыновьям узла t
5 then удаление x
6 смещение сыновей t справа от порцию влево
7 if t имеет одного сына
8 then return TRUE
9 else return FALSE
10
t – внутренний узел, сыновья которого
не листья
11 выбрать w – сына узла t для удаления узла x
12
F T23_Delete1(w,x)
13 if F=FALSE then return FALSE
14
удален один из сыновей узла w и w
имеет одного сына
15 if w – первый сын узла t
16 then if y – второй сын узла t имеет 3-х сыновей
17 then 1-й сын y делается 2-м сыном узла w
18 else сын узла w делается 1-м сыном узла y
19 удаление узла w из сыновей узла t
20 if t имеет одного сына
21 then return TRUE
22 else return FALSE
23 if w – второй сын узла t
24 then if y – первый сын узла t имеет 3-х сыновей
25 then 3-й сын узла y делается 1-м сыном узла w
26 return FALSE
27 if z – третий сын узла t имеет 3-х сыновей
28 then 1-й сын узла z делается 2-м сыном узла w
29 return FALSE
30
первый и третий сыновья узла t не имеют 3-х сыновей
31 сын узла w делается 3-м сыном первого сына узла t-y
32 удаление w из сыновей узла t
33 if t имеет одного сына
34 then return TRUE
35 else return FALSE
36
w – третий сын узла t
37 if y – второй сын узла t имеет 3-х сыновей
38 then 3-й сын узла y делается 1-м сыном узла w
39 return FALSE
40
else узел y
имеет 2-х сыновей
41 сын w делается 3-м сыном узла у
42 удаление w из сыновей узла t
43 return FALSE
Более подробный псевдокод операции удаления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
