Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУВПО
«Комсомольский-на-Амуре государственный
технический университет»
Кафедра «Технология машиностроения»
ОЦЕНка ПОГРЕШНОСТей результатов
косвенных ИЗМЕРЕНИЙ
Методические указания к лабораторной работе № 6 по дисциплинам
«Метрология, стандартизация и сертификация» для студентов
направлений 150300, 150600, 240100,
специальностей 130603, 150106, 190701, 230401, 240801,
«Метрология, стандартизация и взаимозаменяемость» для студентов
специальности 280101,
«Общая теория измерений» для студентов направления 200500
очной формы обучения
Комсомольск – на – Амуре 2009
УДК 389 (075)
Оценка погрешностей результатов косвенных измерений: Методические указания к лабораторной работе № 6 по дисциплинам «Метрология, стандартизация и сертификация», «Метрология, стандартизация и взаимозаменяемость» и «Общая теория измерений»/ Сост. В.В. Алтухова, – Комсомольск – на – Амуре: Комсомольский – на – Амуре гос. техн. ун-т, 2009 – 11 с.
В методических указаниях приведены теоретические сведения по обработке результатов косвенных измерений, даны примеры вычисления погрешности косвенных измерений.
Предназначены для студентов направлений 150300 «Прикладная механика», 150600 «Материаловедение и технология новых материалов», 200500 «Метрология, стандартизация и сертификация», 240100 «Химическая технология и биотехнология» и специальностей 130603 «Оборудование нефтегазопереработки», 150106 «Обработка металлов давлением», 190701 «Организация перевозок и управление на транспорте (водном)», 230401 «Прикладная математика», 240801 «Машины и аппараты химических производств», 280101 «Безопасность жизнедеятельности в техносфере» очной формы обучения.
Печатается по постановлению редакционно-издательского совета Комсомольского – на – Амуре технического университета.
Согласовано с отделом стандартизации.
Рецензент О.И. Медведева
Редактор Е.О. Колесникова
Цель работы: 1) получить навыки обработки результатов косвенных измерений; 2) определить результат косвенного измерения объема втулки.
Оборудование: 1) нутромер; 2) микрометры; 3) втулка; 4) чертеж втулки; 5) стойка.
Введение
Косвенные измерения – это измерения, проводимые косвенным методом, при котором искомое значение физической величины определяется на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
В лабораторной практике большинство измерений – косвенные и интересующая величина N является функцией одной или нескольких непосредственно измеряемых величин:
N=f(x, y, z,…). (1)
Например, объем цилиндра находится по формуле
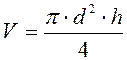 ,
(2)
,
(2)
где d – диаметр цилиндра;
h – высота цилиндра.
Здесь диаметр и высота цилиндра определяются непосредственно измерениями, а объем цилиндра является функцией этих двух непосредственно измеренных величин:
V=f(d, h).
1 Результат прямых многократных измерений
Прямые измерения – это измерения, проводимые прямым методом, при котором искомое значение величины получают непосредственно. Например, измерение длины штангенциркулем или микрометром, угла – угломером.
Из-за погрешностей измерения отдельный измеренный
размер х в общем случае не является истинным значением этой величины. Любое
измерение дает значение измеряемой величины лишь приближенно. Для оценки
точности измерений и получения значений измеряемой величины с определенной
вероятностью необходимо произвести несколько измерений. Результат любых измерений
записывается в виде ![]() .
.
Например, многократные измерения некой величины дали результат 323±1, что означает следующее: истинное значение величины лежит между 322 и 324, а погрешность измерений в данном случае равна 1. Диапазон возможных значений погрешности называют доверительным интервалом (в данном примере границы погрешности равны ±1), а за истинное (действительное) значение измеряемой величины принимают среднее арифметическое.
2 Обработка результатов косвенных измерений
Как следует из теории вероятностей, среднее арифметическое значение величины N, являющейся функцией непосредственно измеряемых величин, определяется подстановкой в формулу 1 средних значений данных величин:
![]() . (3)
. (3)
Погрешность результата измерения величины N, которая не измеряется непосредственно, а вычисляется по измеренным x, y, z,…, находится с применением теории производных и дифференциалов.
Для нахождения случайной погрешности косвенных измерений следует пользоваться формулами:
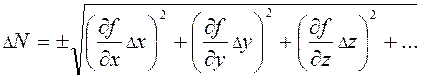 (4)
(4)
и
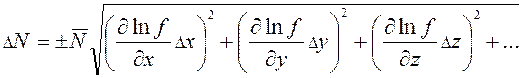 (5)
(5)
где 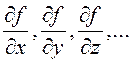 –
частные производные функции N=f(x, y, z,…) по аргументу
–
частные производные функции N=f(x, y, z,…) по аргументу
x, y, z,…, найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;
Δх, Δy, Δz,… – доверительные границы для аргументов x, y, z,….
Формулой (4) удобно пользоваться в случае, если функция N=f(x, y, z,..) имеет вид суммы или разности аргументов. Формулой (5) удобно пользоваться в случае, если функция N=f(x, y, z,…) имеет вид произведения или частного аргументов.
Следует иметь в виду, что доверительные границы Δх, Δy, Δz,…должны быть взяты при одинаковой доверительной вероятности Р.
3 Пример расчета погрешности косвенного измерения
Пример 1. Найти погрешность результата косвенного измерения величины х, связанной формулой
![]() (6)
(6)
со следующими величинами, измеряемыми прямыми способами:
![]() ;
; ![]() ;
; ![]() .
.
Зная, что с2 – р2= (с – р)·(с + р), преобразуем формулу (6):
![]() . (7)
. (7)
Т.к. формула (7) имеет вид произведения, то воспользуемся формулой (5):
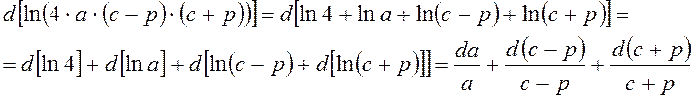 . (8)
. (8)
Раскроем теперь выражения d(c – p) и d(c + p) :
d(c – p)= dc – dp,
d(c + p)= dc + dр.
Тогда выражение (8) примет вид:
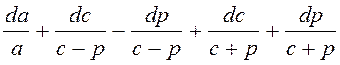 .
.
Затем объединим все члены, содержащие дифференциалы одной и той же переменной:
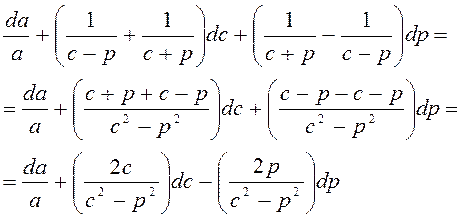
Используя формулу (5), получим выражение для вычисления ошибки измерения величины х:
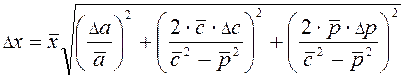 ,
,
где ![]() .
.
Окончательно результат измерения величины х имеет вид:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.