Способы представления алгоритмов функционирования управляющих автоматов, страница 5

Систему формул перехода (СФП) получим выписав формулы перехода поочередно для каждой строки МСА, начиная со строки У₀.

Так из рис.23.4 получим следующую систему формул перехода (СФП)

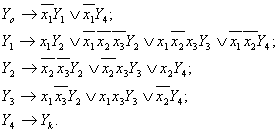 (24.4)

Переход от СФП к ГСА можно выполнить, приведя вначале каждую формулу перехода к минимальной скобочной форме и построив затем подграф для каждой минимальной формулы перехода.

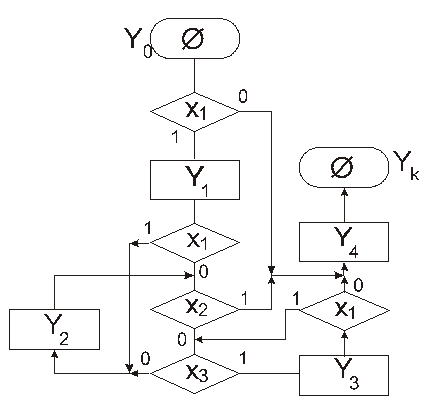
Рисунок 23.4 – Пример ГСА

23.4. Система секвенций

В общем случае Y_t сложного алгоритма (описывающего, например, функционирование автоматизированной системы управления (АСУ)), зависит от конечного числа логических условий {X_i1, …, X_ir}_, принадлежащих множеству Х.

В связи с этим, удобно использовать специализированный язык для задания алгоритмов. К числу таких языков относится система секвенций (СС). Элементарная секвенция определяет условие (перехода) к оператору последователю У_j после оператора предшественника У_i.

Секвенция определяется в форме (23.4)

                                                                           (23.4)

Символ |— означает “если то”. Формулу (23.4) следует понимать таким образом: оператор У_j может быть выполнен после оператора Y_i, если условие Х_ij истинно. Если оператор У_j имеет много операторов предшественников, то секвенция представляется в форме систем секвенций:

                                                   , j=1,…,T.        (23.5)

Примером алгоритма предшественного в форме системы секвенций – СС является следующий алгоритм:

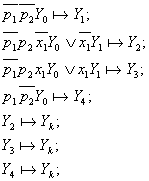                                      (23.6)

Легко видеть,  что СС (23.6) можно получить из МСА, выписав секвенцию для каждого столбца.

Представление алгоритма в форме СС имеет в качестве преимущества компактность представления. От СС можно перейти к МСА и далее к другим формам представления алгоритм-граф-схеме алгоритм (ГСА), логической схеме алгоритма ХСП или к системе формул перехода (СФП).