Цифровые автоматы с неоднородной памятью, страница 7

                                              _{…              …         …              ,}

                             a_R           b_R        P_r

состоящую из всех  пар номеров (a_r, b_r), r=1,R), для которых   p_r =  0.

б) Упорядочиваем строки матрицы Т, для чего строим матрицу М, таким образом, чтобы для нее обязательно выполнялось условие зацепления.

Ø,       r=2,R

и по возможности условия упорядочения весов

                    .

в) Состояния из первой строки матрицы М кодируем парой кодов  с наименьшим возможным кодовым расстоянием

                                       .

г) Вычеркиваем из матрицы М первую строку с полностью закодированными состояниями. Оставшуюся матрицу обозначаем через .

д) В силу условия зацепления в первой строке  закодирован точно один элемент. Выбираем из первой строки  незакодированный элемент и обозначаем его через .

е) Строим матрицу , выбрав из  строки , содержащие g. Пусть   -  множество состояний из  , которые уже закодированы. Пусть - коды этих состояний .

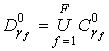ж) Для каждого   найдём - множество кодов  , ещё не занятых для кодирования и имеющих   . Строим множество . Если  , то строим новое множество 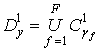 кодов  , для которых