Система MATLAB

изображения Лапласа выходного процесса к изображению Лапласа входного процесса при нулевых начальных условиях.

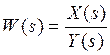,                                                                                                      (9)

где X(s) = L{x(t)}, Y(s) = L{y(t)}.

Отсюда следует простое соотношение между изображениями входного и выходного процесса

X(s) = W(s)Y(s).                                                                                                 (10)

Отсюда, в свою очередь, следует простое правило определения выходного процесса по входному процессу:

1)  определить изображение (преобразование Лапласа) Y(s) входного процесса y(t);

2)  определить изображение X(s) выходного процесса x(t) по выражению (10);

3)  определить оригинал x(t) по изображению X(s).

Определение прямого и обратного преобразования Лапласа в общем случае связано с трудностями аналитического порядка. Однако в инженерной практике основной интерес представляет поведение системы при подаче на вход небольшого числа "типовых" воздействий. Изображения этих воздействий легко вычисляются (или заимствуются из таблиц). Определение изображения выхода по выражению (10) также не представляет труда.

Таким образом, только последний из трех перечисленных пунктов представляет некоторые трудности при вычислении реакции системы на типовые воздействия. Передаточная функция линейной системы (без запаздывания) – дробно-рациональная функция переменной s. Если ограничиться рассмотрением входных сигналов, изображение которых также представляется дробно-рациональными функциями, то изображение выходного сигнала будет иметь такой же вид и при обсуждении вопроса о нахождении обратного преобразования Лапласа можно ограничиться случаем дробно-рациональных функций s. Этот частный случай не представляет принципиальных трудностей.

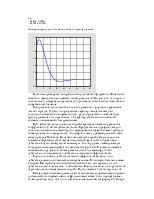
Импульсная переходная функция k(t) – реакция системы на d-импульс. Таким образом, если положить, что входной сигнал y(t) = d(t), то выходной сигнал можно считать равным импульсной переходной функции x(t) = k(t). Известно, что преобразование Лапласа d-функции равно единице L{d(t)} = 1. Из  уравнения (10) следует, что преобразование Лапласа импульсной переходной функции равно передаточной функции L{k(t)} =  W(s) или, что то же самое, что импульсная переходная функция равна обратному преобразованию Лапласа от передаточной функции

k(t) = L^-1{W(s)}.                                                                                                (11)

Таким образом, две основные характеристики линейной системы (импульсная переходная функция и передаточная функция) связаны между собой как пара преобразований Лапласа (оригинал и изображение). Передаточная функция системы легко определяется по дифференциальному уравнению. Однако это функция комплексного аргумента и поэтому качественные суждения о поведении системы для специалистов, не использующих спектральные представления в своей деятельности, представляют значительные трудности. Для суждения о поведении системы во временной области (т.е. по функциям времени) от передаточной функции лучше перейти к импульсной переходной функции.

Для определения импульсной переходной функции по передаточной функции последнюю представляют в виде суммы слагаемых настолько простого вида, чтобы обратное преобразование Лапласа от каждого слагаемого уже не представляло труда. Поскольку данное преобразование линейно, то преобразование Лапласа (прямое или обратное) суммы слагаемых равно