Синтез электрических цепей

непрерывную дробь должно, очевидно, привести к такому результату: 

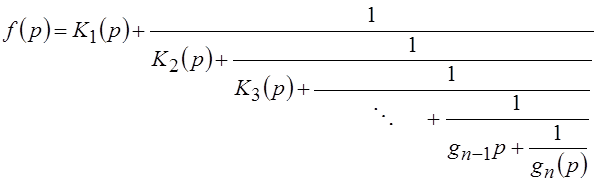                  (46)

Отметим, что все полученные при этом постоянные   являются положительными вещественными числами.

Сравнение выражений (39) и (43) показывает, что, если положить:

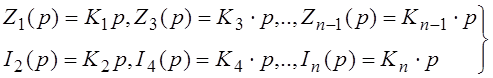                                    (47)

то заданная функция    может быть реализована в виде входного сопротивления цепной схемы, у которой (рис. 12) все последовательные ветви содержат только индуктивности, а параллельные ветви – только емкости. При этом значения   и   определяются полученными величинами  .

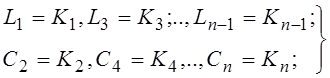                                                               (48)

Схема, изображенная на рис. 12, носит название первой канонической схемы Кауэра.

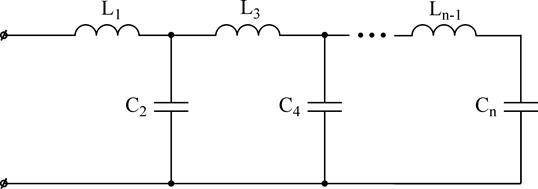
                                                     Рис.12.

При построении этой схемы предпологалось, что функция   является неправильной дробью. Это требование не является обязательным. Если степень полинома числителя А(р) ниже степени полинома знаменателя В(р), то результат первой операции деления можно считать равным нулю, что означает, что индуктивность  должна в данном случае отсутствовать (заменяется коротким замыканием). Емкость  тоже не является обязательным элементом схемы. Она должна присутствовать или отсутствовать (заменяется коротким замыканием) в зависимости от того, является ли точка р=0 соответственно полюсом или нулем функции f(p).

7.3 Вторая каноническая схема Кауэра.

Другой вид непрерывной дроби можно получить, если на каждом этапе разложения стремиться выделить не полюс в бесконечно удаленной точке, а полюс в точке р=0. При подобном подходе заданная функция f(p) записывается в виде

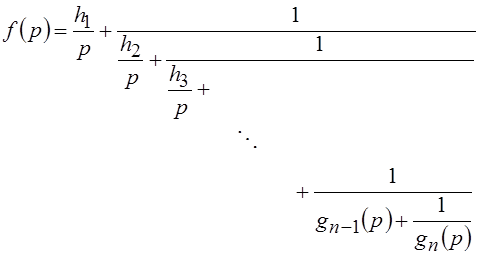                                      (49)

Будем считать, что функция f(p), записанная в виде (49), должна быть реализована в виде входного сопротивления Z(р). Сравним выражения (42) и (49). Из сравнения имеем

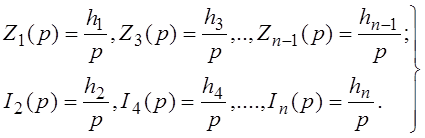                                               (50)

Лестничная схема, реализующая в данном случае  f (p) в виде входного сопротивления, должна, очевидно, содержать емкости в последовательных ветвях и индуктивности в параллельных ветвях (рис 13а). Схема рис 13а называется второй канонической схемой Кауэра

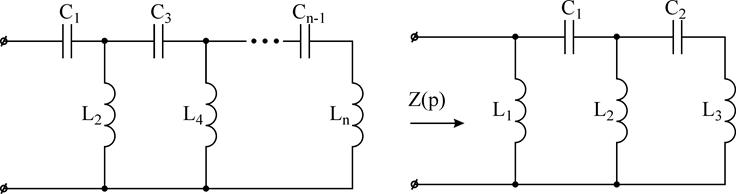
                                                               Рис.13.

а ее элементы при этом должны определятся соотношением

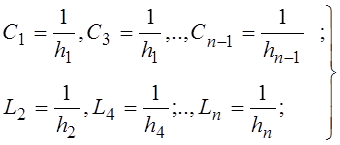                                                              (51)

Как и в предыдущем случае не все элементы этой схемы являются обязательными. Если функция f(p) имеет при р=0 не полюс, а нуль, то в схеме рис 13а, должна отсутствовать емкость  . Индуктивность  должна присутствовать или заменяться коротким замыканием  в соответствии с тем , является ли бесконечно удаленная точка полюсом или нулем функции f(p).

Рассмотрим пример. Требуется реализовать в виде входного сопротивления двух полосной цепи функцию

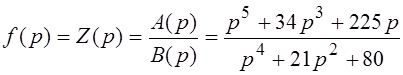
Воспользуемся при решении такой задачи второй схемой Кауэра. Точка р=0 является нулем функции f(p), а не полюсом. Поэтому, начиная построение непрерывной дроби вида (46), следует прежде всего перейти от функции f(p) к обратной величине **** в порядке возрастания степеней переменной и разделить их друг на друга

,

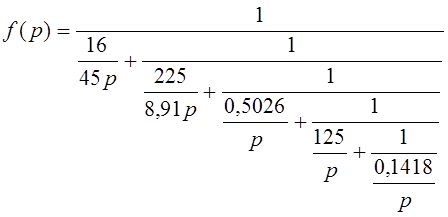где 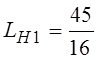; ; 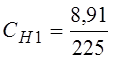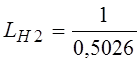*; ; 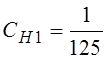 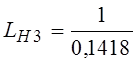- нормированные параметры цепи, так как функция f(p) соответствует входному сопротивлению Z(p) схемы, изображенной на рис.13б. При этом величины емкостей и индуктивностей должны иметь следующие значения: 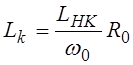, 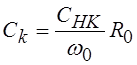. Если f(p)=Y(p), то при разложении в непрерывную дробь в форме (39) получится первая схема Кауэра, если же использовать разложение вида (46), то результатом будет вторая схема Кауэра.

Важным свойством рассмотренных канонических схем Фостера и Кауэра является то, что число элементов, необходимых для их построения, оказывается минимально возможным и равным наибольшему из чисел п и т , где п и т -  степени полиномов А(р) и В(р).

§8 Синтез двухполюсников с потерями (Метод Кауэра)

В общем случае целесообразно выделять каждый раз слагаемые более